Review of Course Computer Vision Lecture 14:Segmentation and Clustering

Review of Course Computer Vision Lecture 14:Segmentation and Clustering

January 05, 2024

为期末考试复习做个准备。

总文章地址。

Lecture 14: Segmentation and Clustering

语义分割要做的任务就是将图像分割成若干个目标。

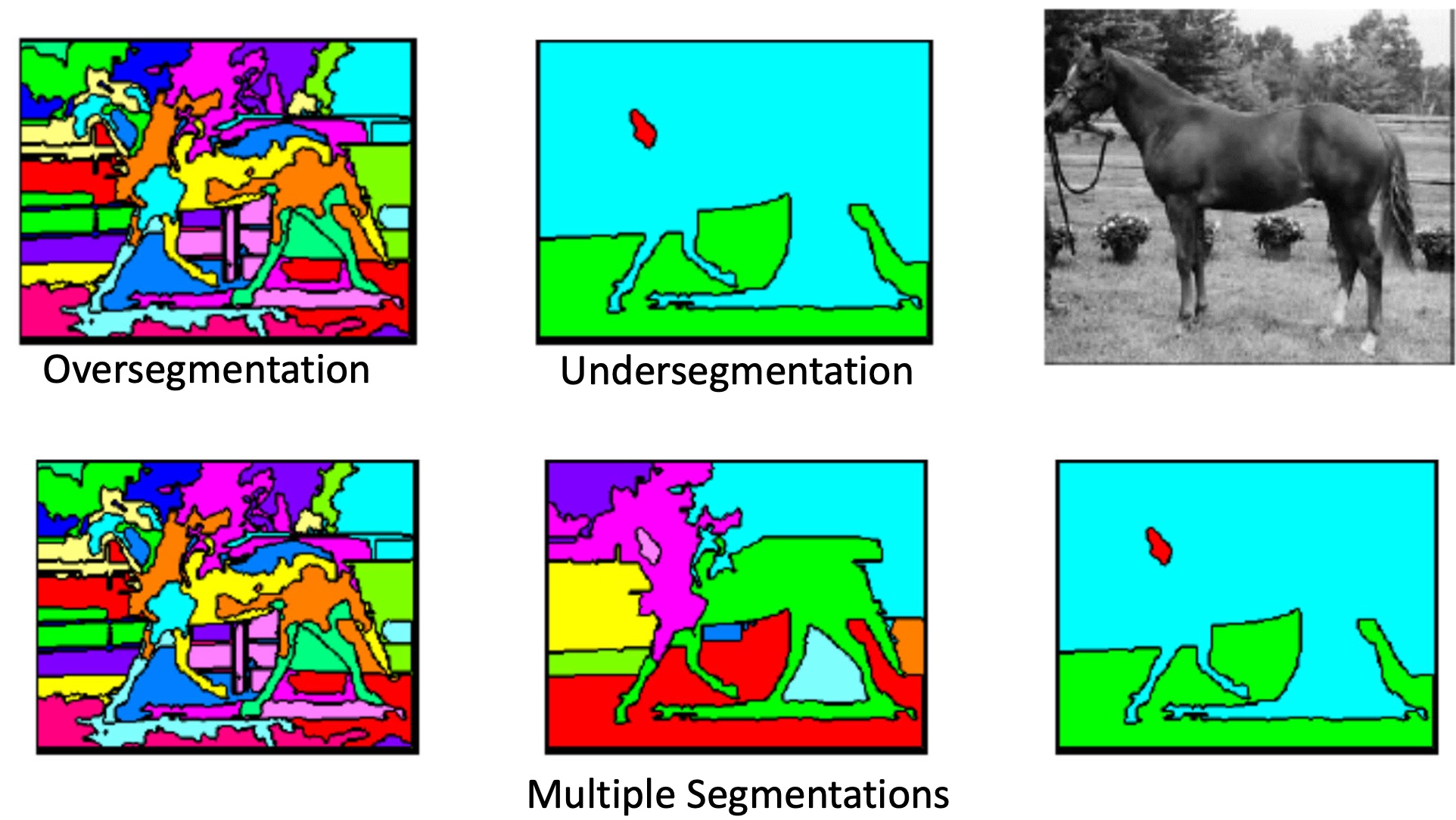
语义分割可以用聚类解决。即若对每个像素点用一些向量描述后，只需要在高维空间聚类，就可以将图像分割一个个部分，就完成了语义分割的任务。

聚类算法：

  1. Agglomerative clustering (层次聚类)：每次选择两个”最近”的类合并。
  2. K-means：迭代，每次以类的中心来吸引更近点。
  3. Mean-shift clustering：基于密度的聚类。

聚类的思路也分两种：

  1. Bottom up clustering：一些 tokens 会被聚在一起是因为它们几乎一致。
  2. Top down clustering：一些 tokens 会被聚在一起是因为它们处于同一个目标中。

语义分割有如下几个基本的原则：

  1. Proximity：物体越接近，那么它们更容易被感知为同一组的。
  2. Similarity：若物体具有相似特征，那么它们更容易被感知为同一组的。
  3. Common Fate (共方向)：若物体向共同方向运动，那么它们更容易被感知为同一组的。
  4. Symmetry (对称)：我们倾向于把不对称，不完全，复杂的图形感知成对称、完全、简单的图形。
  5. Continuity：我们倾向于感知连续，而不是零散。也就是我们会把一些看起来零碎的东西看做是连续的。
  6. Closure (封闭)：哪怕物体不完整（不存在），我们也能根据认知脑补出缺失的部分。

Agglomerative clustering

如何评判两个向量是否相似？一个想法是使用 $L_2$ (欧几里得距离)；另一个想法是利用 Cosine 相似性。也即
$$
\mathrm{dist}(\mathbf{x},\mathbf{x’})=\sqrt{\sum (x_i-x’_i)^2}\\
\mathrm{sim}(\mathbf{x},\mathbf{x’})=\cos\theta=\frac{\mathbf{x}^T\mathbf{x’}}{\Vert \mathbf{x}\Vert\Vert\mathbf{x’}\Vert}=\frac{\mathbf{x}^T\mathbf{x’}}{\sqrt{\mathbf{x^T}\mathbf{x}}\sqrt{\mathbf{x’^T}\mathbf{x’}}}.
$$
聚类算法的几大原则：

  1. Scalability，在时间和空间上有可扩展性。
  2. 可以处理不同类别的数据。
  3. 容易确认输入的参数。
  4. Interpretability and usability，可解释和可用，即可以根据用户需求指定。

层次聚类的想法比较简单。初始时把每个点看成一个类，然后每次选择两个”最近”的类合并，不断更新，就能获得一棵记录了合并过程的树。根据我们的需求来选择树上的某一层即可。

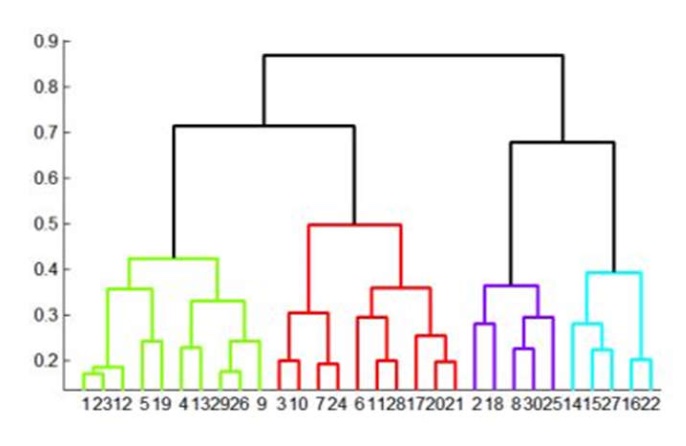
于是我们只需要考虑如何定义两个类的距离，方式比较多，下面介绍四种。

  1. Average distance between points: $d(C_i,C_j)=\frac{\sum_{\mathbf{x}\in C_i}\sum_{\mathbf{y\in C_j}}d(\mathbf{x},\mathbf{x’})}{\lvert C_i\rvert\lvert C_j\rvert}$，又被称为 Average linkage。
  2. maximum distance: $d(C_i,C_j)=\max_{\mathbf{x}\in C_i, \mathbf{x’}\in C_j} d(\mathbf{x},\mathbf{x’})$，又被称为 Complete linkage，它会生成比较胖的类。
  3. minimum distance: $d(C_i,C_j)=\min_{\mathbf{x}\in C_i, \mathbf{x’}\in C_j} d(\mathbf{x},\mathbf{x’})$，又被称为 Single linkage，它会生成比较长条的类，同时可以通过这个类之间的距离来设定是否停止聚类。
  4. Distance between means or medoids: 距离定义为两个类的均值点之间的距离或者中心点之间的距离。

层次聚类的优势：

  1. 应用广泛，实行简单。
  2. 类会有自适应的形状。
  3. 给出了类的层次 (聚类过程树)。
  4. 在一开始不需要限定类的数量。

劣势：

  1. 可能拥有不平衡的类。
  2. 在最后仍需要确定类的数量或者距离阈值来决定类。
  3. 时间复杂度比较糟糕，暴力实现是 $\mathcal O(n^3)$，不过通过一些数据结构优化后可以达到 $\mathcal O(n^2)$。
  4. 会陷入局部最优解。

K-means clustering

对于一些中心情况较为明确的图而言，K-means 往往效果会更好。

它主要就是根据最小化 $\mathrm{SSD}=\sum_{i}\sum_{\mathbf{x}\in C_i}\Vert \mathbf{x}-\mathbf{c}_i\Vert^2$ 来完成聚类，更形式化，我们有

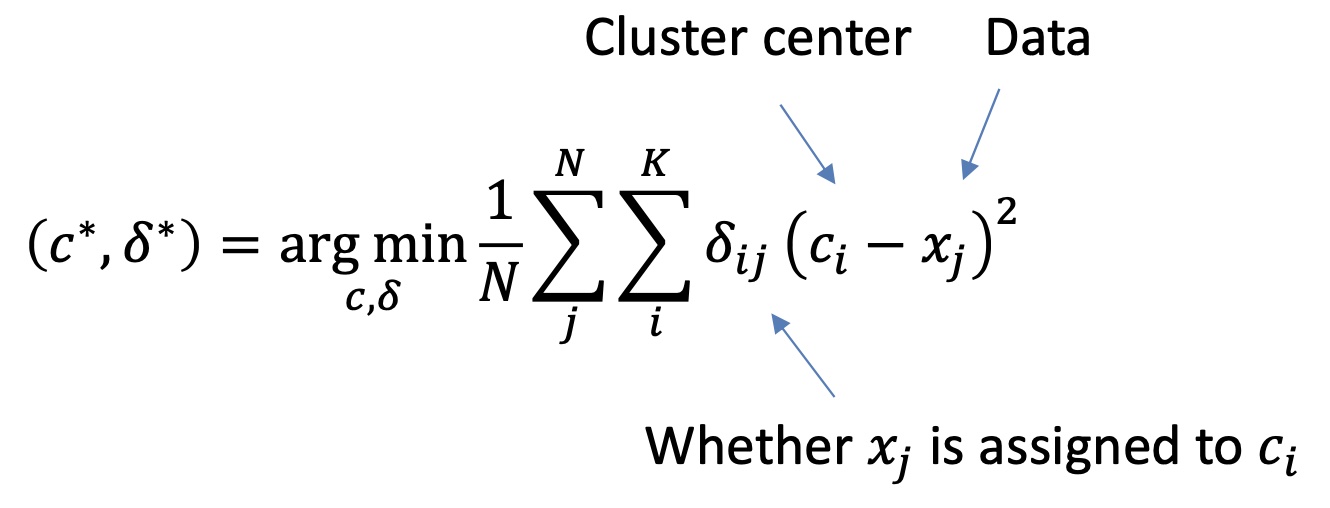
问题就在于，$c$ 被 $\delta$ 确定，这该怎么办呢？对于这种内部循环镶嵌的结构，我们一般使用迭代法。

由于 K-means 较为简单，这里不再做过多赘述。

真实情况中，只要 $c^t$ 变化不动就认为其收敛了。

毫无疑问，K-means 容易收敛到一个局部最优解。同时由于它是到中心的距离来限制，很多时候是更加希望类的形状为球形。$K$ 也需要自己设置，不过很多时候是枚举所有 $K$ 值找最优解。

而对于这些特征的向量选取，有多种方式，比如颜色向量，或者纹理向量 (BoW 类似)，或者像素值加位置向量，第三种综合考量了 similarity 和 proximity。又或者用颜色加位置，这样是考量了更多的 spatial coherence。

K-Means 的优势：

  1. 找到类的中心最小化了条件方差 (每个类能很好地被表达)。
  2. 简单，快速，方便实行。

劣势：

  1. $K$ 要自己选择。
  2. 对局外点敏感 (因为每次是考虑所有点)。
  3. 容易陷入局部最优解。
  4. 要求类的形状为球形，不再自适应。
  5. 每个类的参数一致 (距离函数不是自适应的)。

Mean-shift clustering

Mean-shift 聚类的主要思路是密度聚类，对于每个点我们会用一个圆形窗口来估计密度最大的方向，不断往那个方向移动。

核密度函数为 $\hat{f_h}(x)=\frac{1}{nh}\sum_{i=1}^n K(\frac{x-x_i}{h})$，其中 $K$ 为核函数，一般取高斯核函数，即 $K(x)=\frac{1}{\sqrt{2\pi}\sigma^d}e^{-\frac{\Vert x\Vert^2}{2\sigma^2}}$，其中 $h$ 为圆形 (球体) 窗口的半径，$n$ 为窗口内检测出的点数，$d$ 是维度，一般 $\sigma$ 取 $1$。

根据核密度函数，我们想要往密度最大的方向移动，就是将核密度函数求梯度。不妨设 $K(x)=k(\Vert x\Vert^2), g(x)=-k’(x)$, 于是得到
$$
\nabla \hat{f_h}(x)=\frac{2}{h^2}[\frac{\sum_{i=1}^n g(\Vert \frac{x_i-x}{h}\Vert^2)}{nh}][\frac{\sum_{i=1}^n (x_i-x)g(\Vert \frac{x_i-x}{h}\Vert^2)}{\sum_{i=1}^n g(\Vert \frac{x_i-x}{h}\Vert^2)}].
$$
前面的部分都是常量，后面是均值向量，所以我们会沿着后面那部分移动中心点，即偏移向量是
$$
m(x)=\frac{\sum_{i=1}^n (x_i-x)g(\Vert \frac{x_i-x}{h}\Vert^2)}{\sum_{i=1}^n g(\Vert \frac{x_i-x}{h}\Vert^2)}.
$$
偏移后的位置为 $m(x)+x=\frac{\sum_{i=1}^n x_ig(\Vert \frac{x_i-x}{h}\Vert^2)}{\sum_{i=1}^n g(\Vert \frac{x_i-x}{h}\Vert^2)}$。

具体步骤：

  1. 初始化圆球窗口 $W$，大小为 $h$。
  2. 对于每一个点: (1) 以这个点为中心用窗口检测 (2) 根据 $m(x)$ 获得新的中心点 (3) 以新的中心点检测 (4) 重复 (2)(3) 直到收敛。
  3. 对于抵达相同中心点的点归为同一类。

Mean-shift clustering 优势：

  1. 通用且应用独立。
  2. 聚类对类的形状毫无限制，可以检测出任何形状。
  3. 只需要一个参数 $h$，且 $h$ 有物理意义。
  4. 能找到不同的类。
  5. 对局外点有鲁棒性。
  6. 适合 Oversegmentation, Multiple segmentations, Tracking, clustering, filtering applications。

劣势：

  1. 结果依赖于 $h$。
  2. $h$ 的选择并不容易。
  3. 计算时的时间复杂度较高。
  4. 高维不太适合。

Graph-based segmentation

图聚类的想法是，如果考虑任意两个点的边权是距离相关的某个值的话，求最小生成森林可以被理解为聚类算法等。

我们考虑合并两个连通块 (类) 的要求是什么。

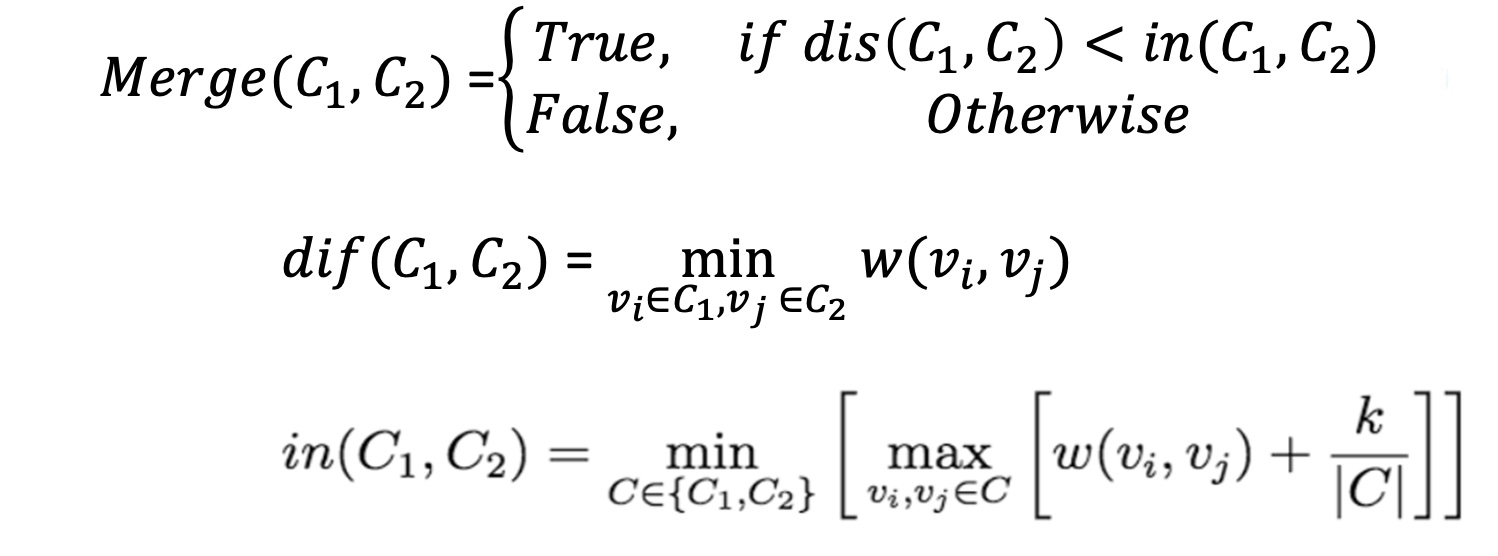
当 $\mathrm{Merge}(C_1,C_2)$ 是 True 的时候就代表可以合并 $C_1, C_2$。图中的 $\mathrm{dif}$ 是打错了，实际应该为 $\mathrm{dis}$。$\mathrm{dis}$ 求的是两个连通块 (类) 之间的最短距离，而 $\mathrm{in}$ 实际上表示的是两个连通块自己内部最大的边权加上某一个阈值，其中 $k$ 为某一预先设置的参数。

我们能理解这个合并。如果自己这一类内部的合并难度就已经大于与其他类合并的话，那肯定会想着与其他类合并。在 $k$ 这一阈值的限制下，给予了更多合并的机会。$k$ 小的时候，会要求类较小；$k$ 大的时候，会要求类较大。

对于图的构建，一种经典的思路是，每个像素点认为是 $(r,g,b,x,y)$ 五维向量，与和它邻域内的点连边，边权使用 $L_2$ 即欧几里得距离来描述，一般连边选择邻域内边权最小的十个点。

  1. 1. Lecture 14: Segmentation and Clustering
    1. 1.1. Agglomerative clustering
    2. 1.2. K-means clustering
    3. 1.3. Mean-shift clustering
    4. 1.4. Graph-based segmentation