Review of Course Computer Vision Lecture 7:Feature Detector
为期末考试复习做个准备。
Lecture 7: Feature Detector
我们想要完成图像匹配的事情,比如有一个建筑物在两张不同的图中都出现了,我们要匹配上这两张图中的建筑物。
又或者我们想拍摄全景图,此时需要合并两张相邻的图,那么就要完成提取特征再特征匹配后,把这些特征点位置对应上,然后将图像融合在一起。
还有许多用处,这里不再赘述。
局部特征比起全局特征的优势在于,局部特征在被遮挡、运动等时候上依旧能保持相应的特征,而全局特征更考察整体的色度等,容易随着图像变化而发生比较大的变化。
局部特征的优势:
- Locality:对于遮蔽的鲁棒性。
- Quantity:一张图像内有成百上千。
- Distinctiveness:比较能在大的图像库里能识别出来。
- Efficiency:能够实时使用。
于是特征点需要在一些变化下保持不变,比如 translation, rotation, scale, brightness, exposure 等。
目标:可重复性检测;精确地局部化;比较能作为区分的点。
实际上可以看作寻找二维函数的信号变化。
Harris corner detection
第一步是寻找 Corners。
Corners 是可重复和可区分的。一般使用一个滑动的窗口来寻找 Corners。



窗口的思路在于将窗口里的每个像素点和某个位移后的窗口作差平方后加权和,以这个数值来判断是否为 Corners,即
$$
E(u,v)=\sum_{x,y} w(x,y)(I(x+u,y+v)-I(x,y))^2.
$$
其中 $(u,v)$ 为位移量,$I(x,y)$ 是 $(x,y)$ 这个点的像素值,$w(x,y)$ 为某一加权函数。

如何证明正确性?考虑 Taylor 展开,即 $I(x+u,y+v)\approx I(x,y)+(\frac{\partial I}{\partial x},\frac{\partial I}{\partial y})(u,v)^T$,不妨假设 $w(x,y)$ 为常值函数,于是
$$
E(u,v)=\sum_{x,y} w(x,y)(I(x+u,y+v)-I(x,y))^2\\
\approx \sum_{x,y} (\frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v)^2\\
=u^2\sum_{x,y} (\frac{\partial I}{\partial x})^2+v^2\sum_{x,y} (\frac{\partial I}{\partial y})^2+2uv\sum_{x,y} \frac{\partial I}{\partial x}\frac{\partial I}{\partial y}\\
=\begin{pmatrix}u & v\end{pmatrix}\begin{pmatrix}A & B\\B & C\end{pmatrix}\begin{pmatrix}u & v\end{pmatrix}^T.
$$
其中,$A=\sum_{x,y}(\frac{\partial I}{\partial x})^2, B=\sum_{x,y}\frac{\partial I}{\partial x}\frac{\partial I}{\partial y}, C=\sum_{x,y} (\frac{\partial I}{\partial y})^2$。
Thus,$E(u,v)$ is locally approximated as a quadratic error function。
设中间矩阵为 $H$,我们能有以下的一些情况。

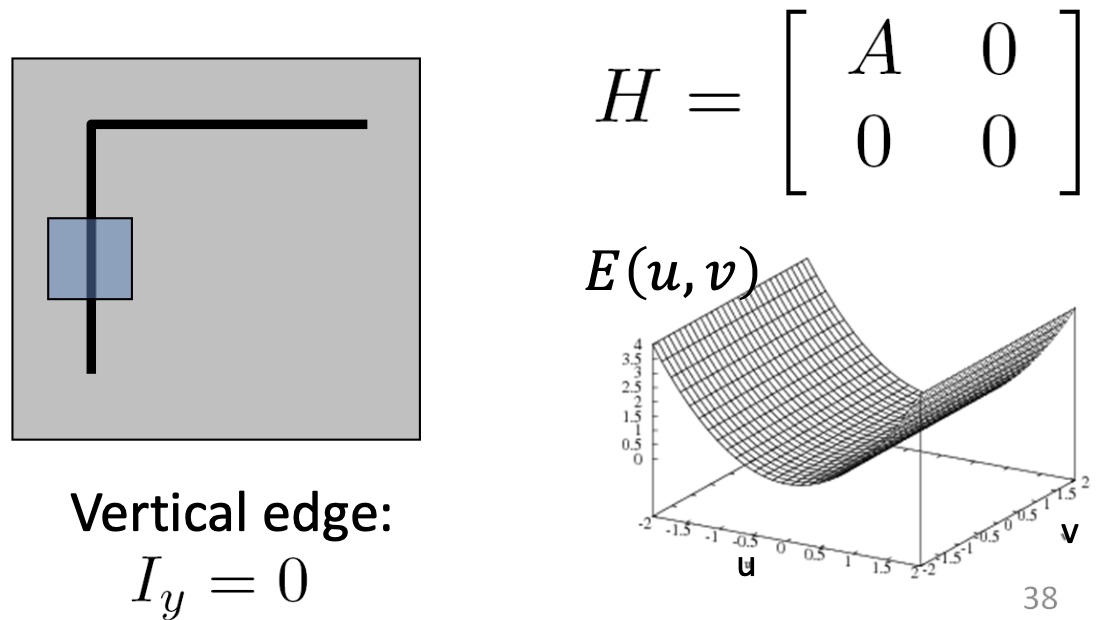

注意到 $H$ 是实对称矩阵,所以其一定能被对角化,即 $H=R^{-1}\begin{pmatrix}\lambda_1 & 0\\0 & \lambda_2\end{pmatrix}R$。旋转图像显然不会改成特征值。

于是就可以根据 $\lambda_1$ 和 $\lambda_2$ 来判断区域情况了。
真实情况中我们不可能对这个矩阵去求出特征值,所以会利用行列式和迹。
$2\times 2$ 的矩阵的行列式和迹是容易求的,即 $\det(H)=h_{1,1}h_{2,2}-h_{1,2}h_{2,1}, \mathrm{trace}(H)=h_{1,1}+h_{2,2}$。
此时利用 $\det(H)$ 和 $\mathrm{trace}(H)$ 的一些运算来获得一些判断规则,比如
$$
\theta=\det(H)-\alpha \mathrm{trace}^2(H),\\
R=\frac{\det(H)}{\mathrm{trace}(H)+\epsilon}.
$$
等等。其中,$\alpha$ 一般取 $0.04$ 到 $0.06$ 之间的某个常数。


Harris corner detection 满足 Translation invariance, Rotation invariance, Partially invariant to affine intensity change, Not invariant to image scale。
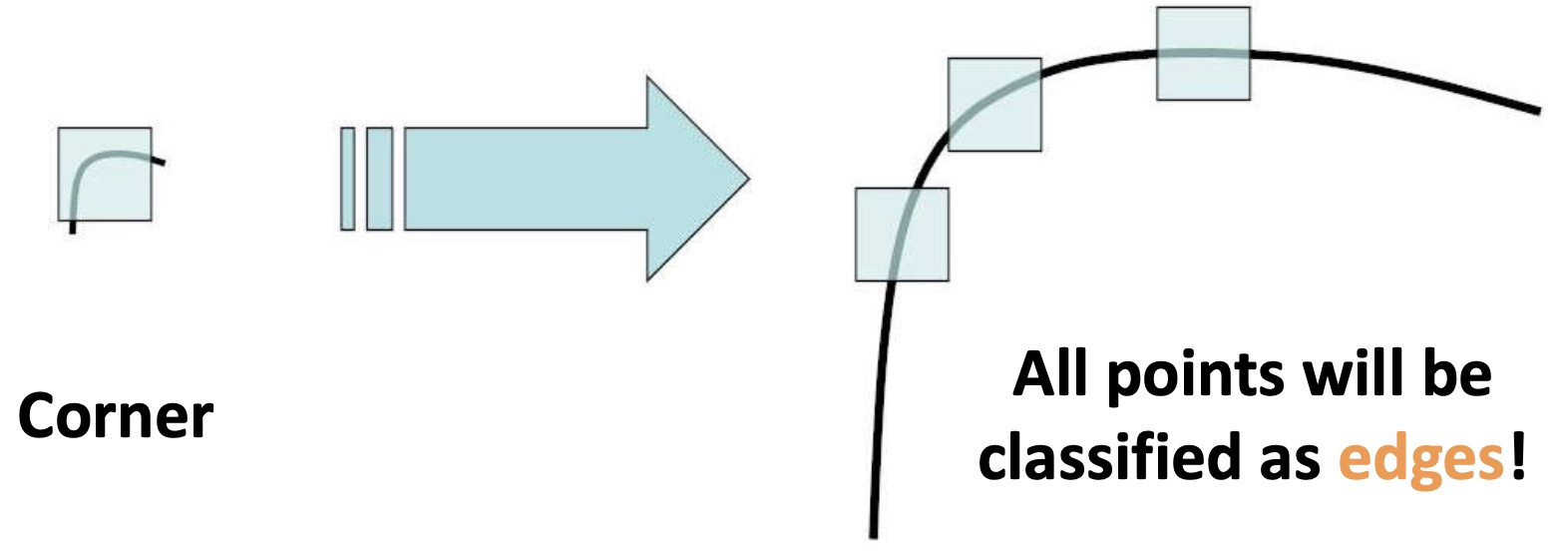
上图可见,尺度变化确实会影响检测。需要我们再次发明尺度不变的检测方法。
Scale invariant detection
高斯相关的卷积核都是保持尺度不变性的。
一种方法被称为 SIFT,构建的是多组多层的高斯差分金字塔,每一组内的图像大小相等,但尺度不同,不同组间由下采样构成,卷积核使用高斯差分函数。在不同层考虑寻找局部最大值 (自己这一层相邻的八个,上一层的九个,下一层的九个),将其作为一个局部特征点,记为三元组 $(x,y,\sigma)$,$\sigma$ 为那一层的尺度 (scale)。这些特征点用来备选,以其他一些方法进行拟合或者删除部分。

另一种方法构建的是 Harris-Laplacian 金字塔,卷积核使用拉普拉斯函数,层内使用 Harris detector 来寻找特征点。对于这些点,类似高斯差分金字塔的办法,若不是局部最大值,则去除。