Review of Course Computer Vision Lecture 15:Motion
为期末考试复习做个准备。
Lecture 15: Motion
视频中的每个像素等价于三维坐标 $(x,y,t)$,表示在图像的 $(x,y)$ 位置,时间为 $t$。
光流: 图像中带光图案的明显运动。
光流不一定是物体运动,也可能是光的运动。
我们想要基于光流,来恢复每个物体的运动情况。
想要分析光流,我们一般基于以下三个假设:
- Small motion:点的移动幅度不会太大。
- Spatial coherence:空间上是一致的,每个点的移动会和它附近的点类似。
- Brightness constancy:每个点在不同时间的像素值是相同的。
Brightness constancy
第三个条件比较强硬,它带出了一个整体性的条件。利用 Taylor 展开,我们有
$$
I(x,y,t)=I(x+u(x,y),y+v(x,y),t+1)\approx I(x,y,t)+[I_x,I_y,I_t][u,v,1]^T\\
\implies I_xu+I_yv+I_t\approx 0\\
\implies \nabla I(x,y) [u,v]^T+I_t\approx 0.
$$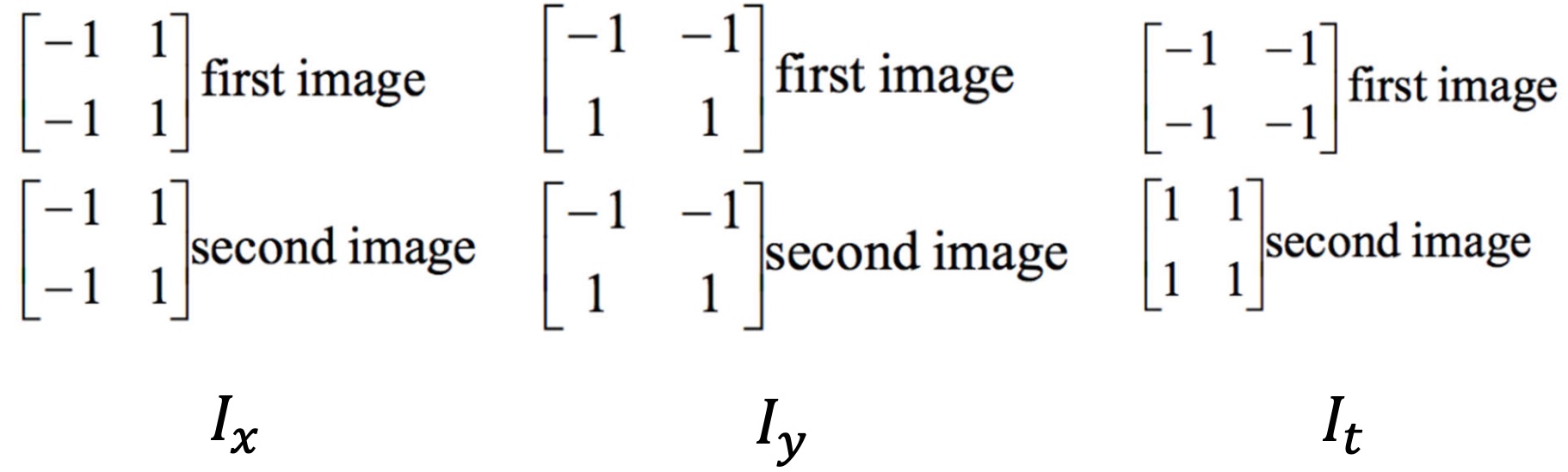
可以发现方程的未知数有两个 $u,v$,但方程只有一条,这意味着会解出若干个解,那也就很难获得光流了。
如何解决这个问题就是重中之重,我们想办法添加一些方程?
Spatial coherence
根据 Spatial coherence,我们可以假定像素邻域内所有点的光流都是相同的 $(u,v)$,于是能写出一条方程。
假设我们使用的是 $5\times 5$ 的窗口,则有
$$
\nabla I(p_i) [u,v]^T+I_t(p_i)=0.
$$
容易写成某种矩阵的形式,并尝试做出解析解,即

这条方程被称作 Lucas-Kanade equation,其若要有解则需要:
- $A^TA$ 要求可逆。
- $A^T A$ 不能太小,即两个特征值都不能太小,这是因为噪声所以必须要这一点。
- $A^TA$ 的特征值之比不能太大,这里的比值要求大的特征值作为分子。
可以发现这个方程有点类似于 Harris Corner Detector 中的方程。

上图为 Harris Corner Detector 的 $\lambda_1,\lambda_2$ 要求的特征和 Corner 处的比较相似。
Small motion
光流还有一个假设,即 Small motion,我们来分析一下这个假设。
Small motion 也可以被写成一条方程,即
$$
0=I(x+u,y+v)-I_t(x,y)\approx I(x,y)+I_xu+I_yv-I_t(x,y).
$$
牛顿迭代法可以解决这个问题,不过超出了课程内容,这里使用 Lucas-Kanade equation 姑且解决一下。
Lucas-Kanade equation 可以被看作是只迭代了一轮的牛顿迭代法,步骤如下:
- 利用 Lucas-Kanade equation 计算每个像素点的速度 $(u,v)$。
- 利用上面算出的速度来进行图像扭转 (warping),从 $I(t-1)$ 扭转到 $I(t)$。扭转到的像素利用 Small motion 得到。
- 重复步骤,直到收敛。因为不一定整张图像同时成立,而且有损失。
接下来讨论 Lucas-Kanade equation 的损失情况。
产生损失的原因:
- 我们假定了 $A^TA$ 是可逆的,但实际上不一定可逆。
- 我们假定了没有噪声。
- 光流的三大假设不一定都满足,比如 Spatial coherence 选取的窗口大小没法任意,需要调整以获得合适的大小。
Pyramids for large motion
我们先尝试解决 Small motion 失效的情况。
很明显,所有的 Small 和 Large 是和分辨率相关的,所以有一个想法就是改变分辨率,于是会使用高斯金字塔。

Horn-Schunk method
Horn-Schunk 的主要思路是引入了平滑性假设,然后最小化全局能量函数。定义全局能量函数为
$$
E=\int\int [(I_xu+I_yv+I_t)^2+\alpha^2(\Vert \nabla u\Vert^2+\Vert \nabla u\Vert^2)]\mathrm{d}x\mathrm{d}y.
$$
第一部分是 Brightness constancy,第二部分是 smoothness constraint (平滑性假设),$\alpha$ 是某一参数,来平衡二者的。
平滑性假设的引入是考虑了 Spatial coherence 的思路,像素函数越简单就越会让 Spatial coherence 成立,那么根据 Taylor 展开,我们会想到让高阶导数尽量不存在,所以有了这样的假设。这里是让二阶导尽量小。
最小化 $E$ 的方式显然是求导,最终得到
$$
I_x(I_xu+I_yv+I_t)=\alpha^2 \nabla^2 u\\
I_y(I_xu+I_yv+I_t)=\alpha^2 \nabla^2 v
$$
注意到又遇见了 $\nabla^2$ 这个拉普拉斯算子,离散情况下我们可以使用邻域的均值减去自己获得,即
$$
\nabla^2 u(x,y)=\overline{u}(x,y)-u(x,y).
$$
代入后,得到最终表达式:
$$
(I^2_x+\alpha^2)u+I_xI_yv=\alpha^2 \overline{u}-I_xI_t\\
I_xI_yu+(I^2_y+\alpha^2)v=\alpha^2 \overline{v}-I_yI_t
$$
当然,因为 $\overline{u}$ 和 $u$ 之间互相限制,方便的解法是迭代(实际上可以做消元等等),于是有迭代方程:

Michael Black method 在 Horn-Schunk method 的基础上,将 $\Vert \nabla u\Vert^2+\Vert \nabla u\Vert^2$ 更改成了另一个函数,这里不再赘述。
Motion Segmentation
基于语义分割,我们重新考虑 motion。
Affine motion: 仿射运动给出了比较简单的公式:
$$
u(x,y)=a_1+a_2x+a_3y\\
v(x,y)=a_4+a_5x+a_6y
$$
代入 Brightness constancy,则有
$$
I_x(a_1+a_2x+a_3y)+I_y(a_4+a_5x+a_6y)+I_t=0.
$$
于是能定义损失函数为
$$
E(\vec{a})=\sum [I_x(a_1+a_2x+a_3y)+I_y(a_4+a_5x+a_6y)+I_t]^2.
$$
利用上述信息,我们考虑每个 layer 的 motion 情况:
- 将图像分块,利用 $E$ 损失函数计算每个块的仿射运动情况,这样能排除高的残差损失。
- 将每个 motion 映射到 motion 参数空间。

- 执行聚类算法 (K-means) 以完成语义分割工作。

- 让每个像素点归于最佳的物体。
- 执行区域的滤波以满足 spatial constraints。
- 重新每个区域的仿射运动。
- 重新执行 4, 5, 6。

Motion 的应用广泛,比如检测 3D 建筑,检测物体运动,移动物体的语义分割,合成动态纹理,一组图像更改成超分辨率,认知事件和活动。