Review of Course Computer Vision Lecture 3:Resampling and Interpolation
为期末考试复习做个准备。
Lecture 3: Resampling and Interpolation
朴素下采样: 删除原图像的偶数行列。
走样 (Aliasing,又被称为锯齿): 图像信息的损失,绝大多数情况都会产生锯齿形状的图形。
朴素下采样会带来走样的结果,可以以一个 $\sin(x)$ 举例。
时间走样 (Temporal aliasing): 对视频进行一个固定点采样时,会不知道该点的真实运动情况。比如采样的频率过低但圆盘转动过快,容易判断错误顺逆时针。
反走样 (Anti-Aliasing, 又被称为抗锯齿): 几种方法可以抗锯齿,如超采样 (Over-sampling/Super-sampling),思路是将一个物理像素在逻辑上划分多个子区域,然后对这些子区域的中心进行采样,相当于在逻辑上增加了像素点。另一种方法是经典的 Smooth 思想,将原图像模糊化,模糊的程度达到 Nyquist 限制即可。
高斯金字塔
通过 Filter 再 Downsampling 不断压缩图像信息而获得的图像集合们,即
$$
G_{i+1}=\text{Downsampling}(\text{Filter}(G_i)).
$$
高层图像的每个位置是相邻大区域的信息整合,不可复原回原图像,差分可以获得原图像的轮廓 (类似 SIFT 中的特征点)。

为了无损构造金字塔,提出了拉普拉斯金字塔。
拉普拉斯金字塔
想法是差分,存储差分图像,即
$$
H_i=G_i-\text{Filter}(G_i)\\
G_{i+1}=\text{Downsampling}(\text{Filter}(G_i))
$$
其中,$G$ 是高斯金字塔,而 $H$ 则是拉普拉斯金字塔,通过上采样时插值可以一直得到上一层的 $G$。
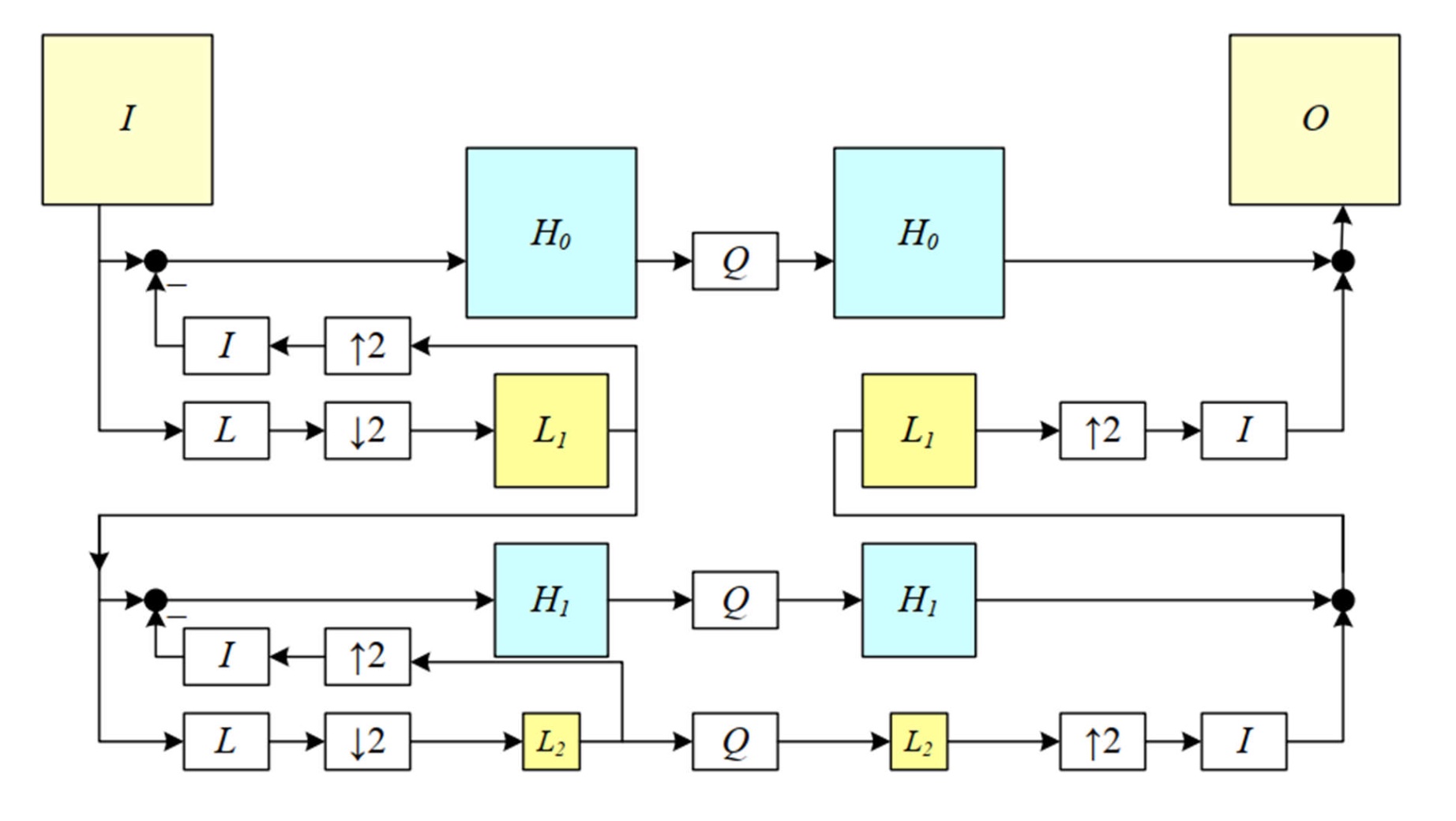
图中的 $L$ 是我描述中的 $G$。
为什么被称为拉普拉斯金字塔?主要是高斯差分函数可以被近似为拉普拉斯算子。
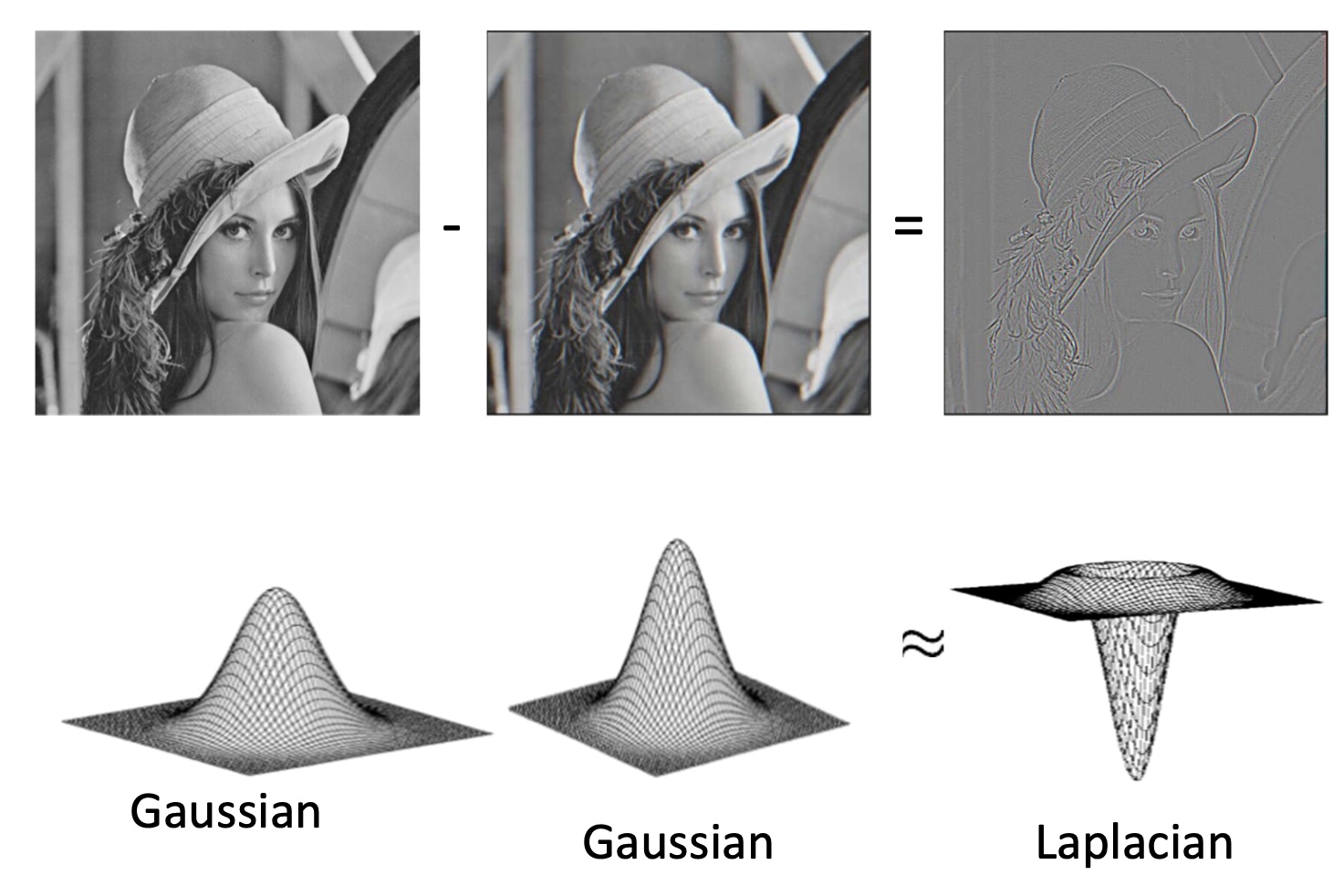
Proof (以前在 SIFT 时证明过):
考虑一个尺度归一化拉普拉斯高斯算子 $\sigma^2\nabla^2$,我们可以推导出
$$
\frac{\partial G}{\partial \sigma}=\frac{-2\sigma^2+x^2+y^2}{2\pi \sigma^5}e^{-(x^2+y^2)/2\sigma^2}\\
\nabla^2 G=\frac{\partial^2 G}{\partial x^2} + \frac{\partial^2 G}{\partial y^2}=\frac{-2\sigma^2+x^2+y^2}{2\pi \sigma^6}e^{-(x^2+y^2)/2\sigma^2}
$$
于是就有 $\frac{\partial G}{\partial \sigma}=\sigma\nabla^2$.
另一方面,我们考虑导数定义,即
$$
\frac{\partial G}{\partial \sigma}=\lim_{\Delta\sigma\to 0} \frac{G(x,y,\sigma+\Delta\sigma)-G(x,y,\sigma)}{(\sigma+\Delta\sigma)-\sigma}.
$$
为了能方便地获得较好的近似解,我们考虑用差分替代微小变量,即
$$
\frac{\partial G}{\partial \sigma}\approx \frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma}\implies G(x,y,k\sigma)-G(x,y,\sigma)\approx (k-1)\sigma^2\nabla^2 G
$$
于是就可以使用高斯差分函数来替代尺度归一化的拉普拉斯高斯函数了。
还有一些其他种类的金字塔,这里不做具体描述。

金字塔的作用较多,如图像压缩,多尺度目标检测,多尺度纹理映射,图像融合等等。
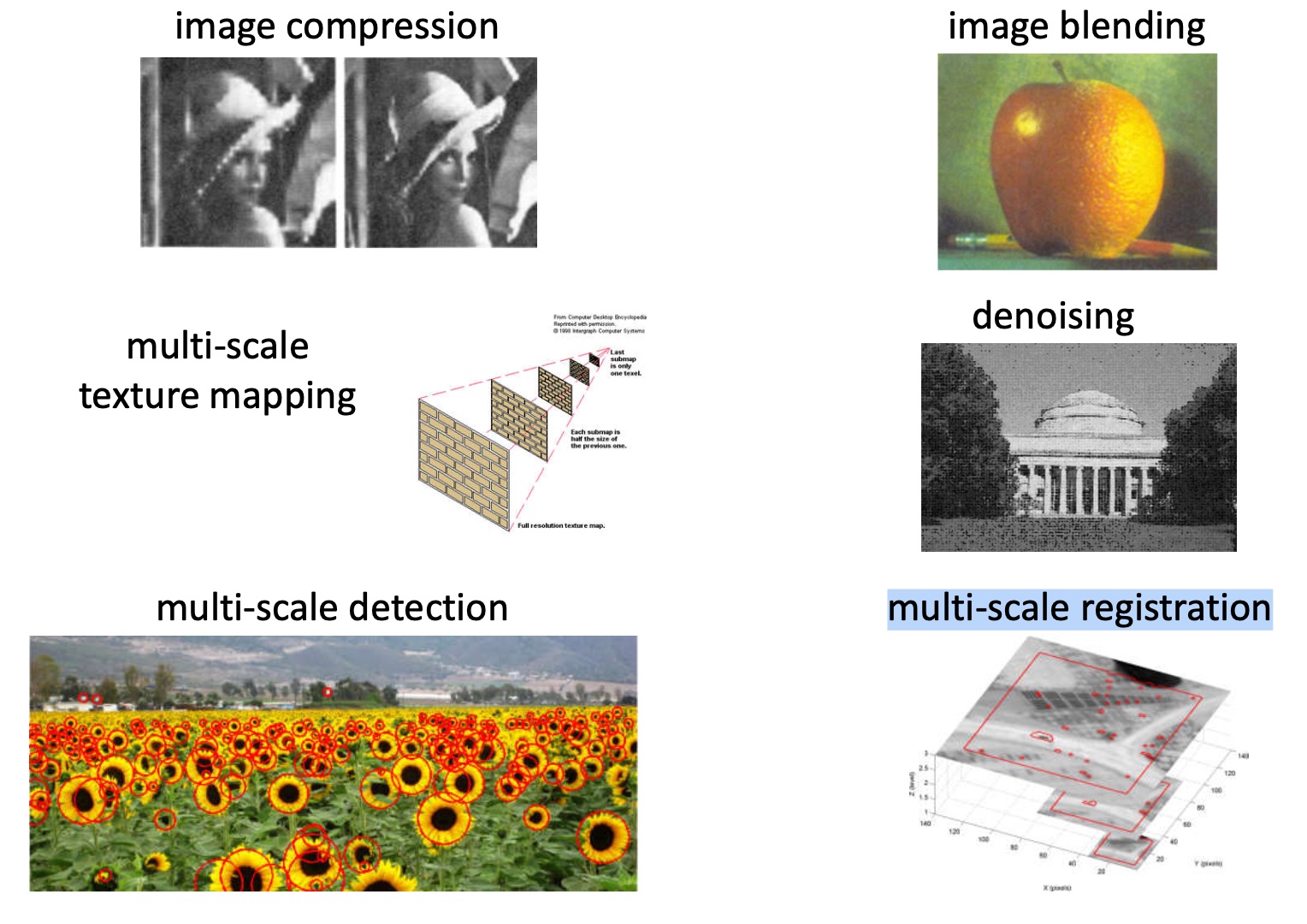
傅立叶理论
傅立叶的思路在于任意函数都可以被一个三角函数级数所表示。
为了能更好地表达这个级数的信息,只需要去存储频率和幅值。使用傅立叶变换的方式。傅立叶变换的主要原因是三角函数彼此之间的正交性,保证了卷积可以变成乘法。
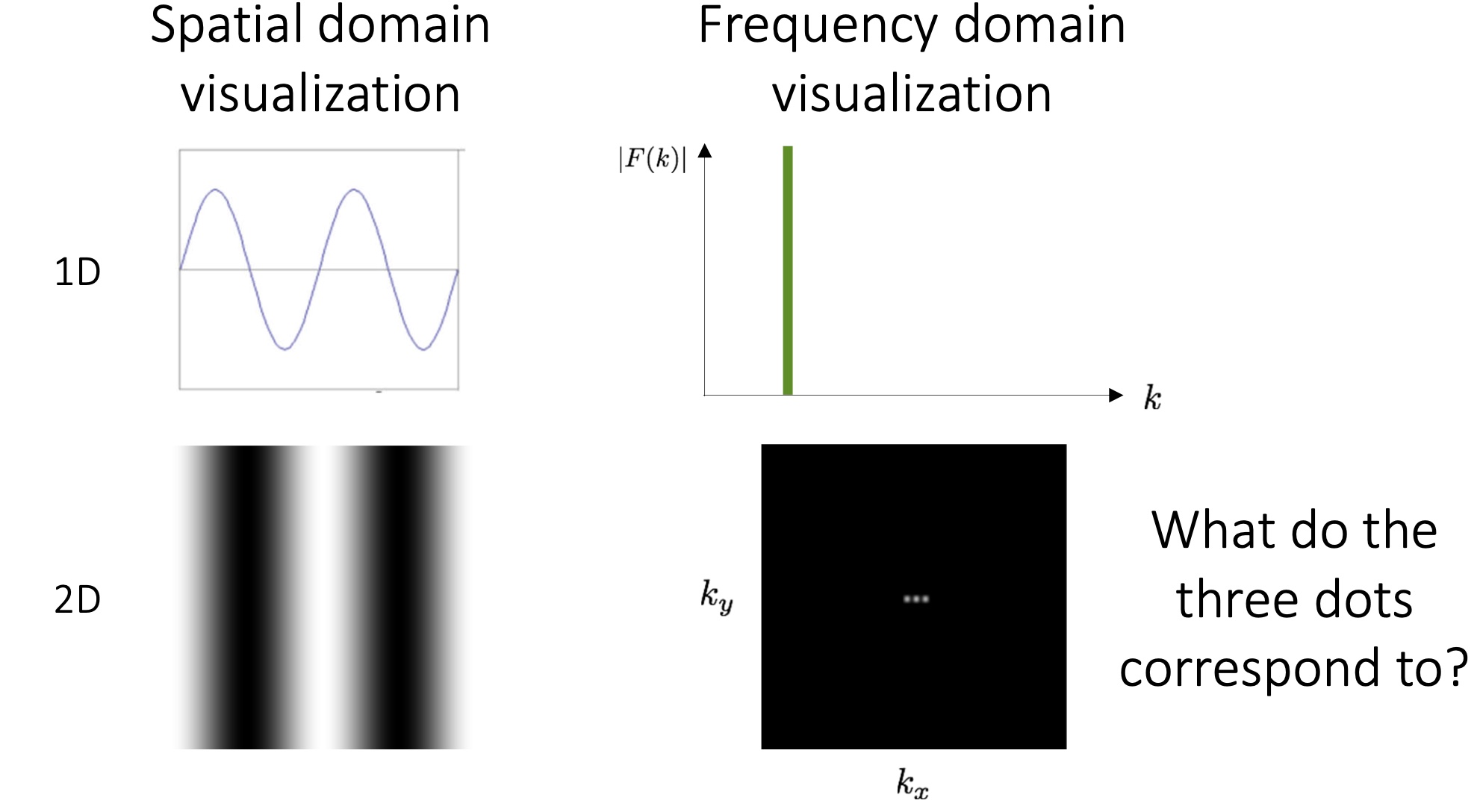
左为空间域的图,右为频域的图。右图中,对 2D 情况,越靠近中间则频率越低,越亮则表示幅值越高 (用 2D 图像表示了 3D 的函数情况,$(\omega_x,\omega_y,f(\omega_x,\omega_y))$)。因此那三个点就表示了傅立叶级数中的三个频率,亮度表示了它们的幅值。
傅立叶变换具有可加性,即设 $\mathcal{F}$ 为傅立叶变换,则 $\mathcal{F}(A+B)=\mathcal{F}(A)+\mathcal{F}(B)$。
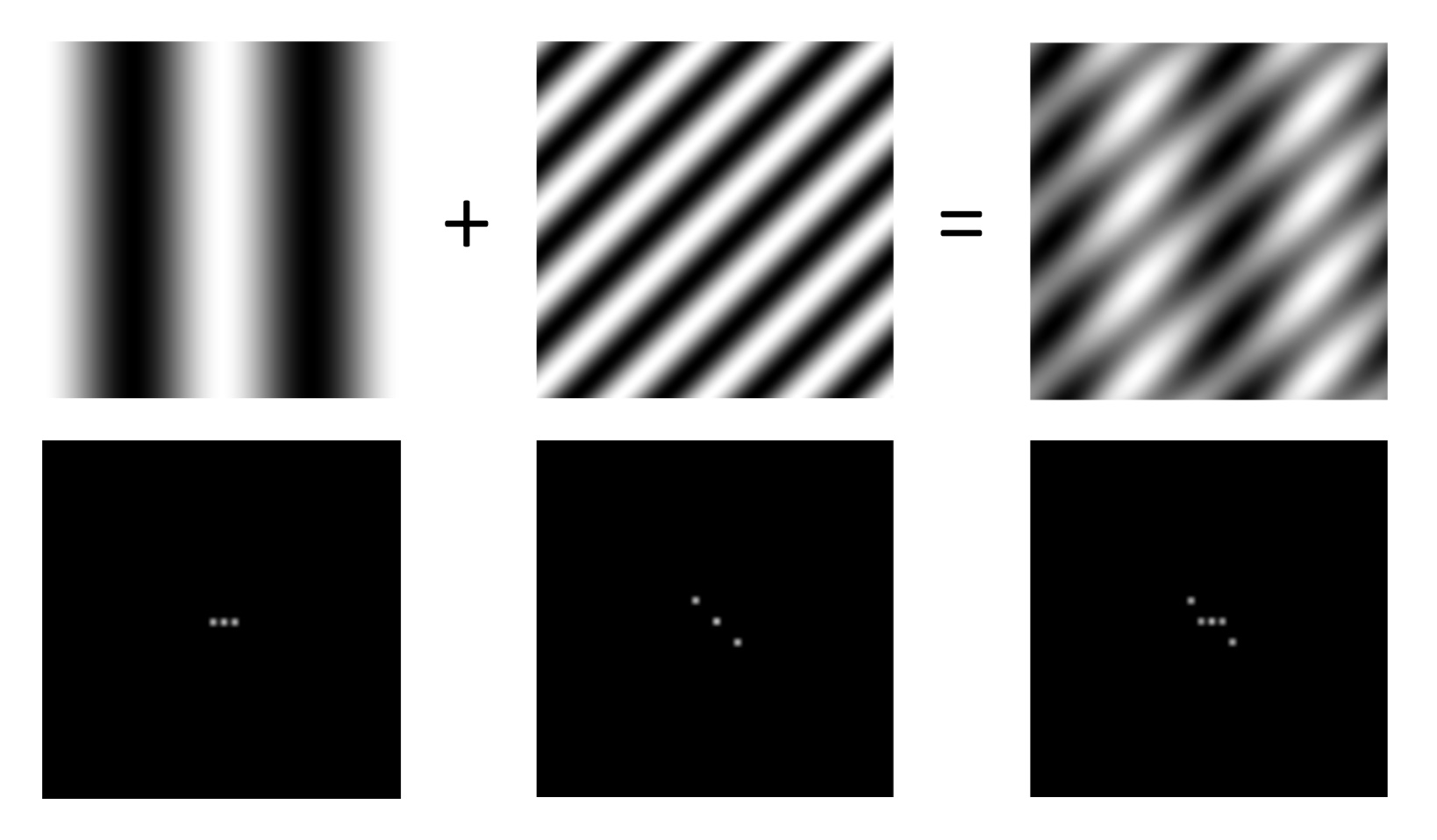

实际上表达式离散傅立叶变换都可以被表示称矩阵乘法的形式,利用范德蒙德矩阵和蝴蝶变换等可以做到 $\mathcal O(N\log N)$ 求出傅立叶变换,被称为快速傅立叶变换 (FFT)。傅立叶变换具有对偶性 (duality)。
傅立叶变换的经典思路是卷积转成乘法,即
$$
\mathcal{F}(A\ast B)=\mathcal{F}(A)\mathcal{F}(B)\\
\mathcal{F}^{-1}(A B)=\mathcal{F}^{-1}(A)\ast\mathcal{F}^{-1}(B)\\
$$
从傅立叶变换的角度下,重新看待 Filter,即
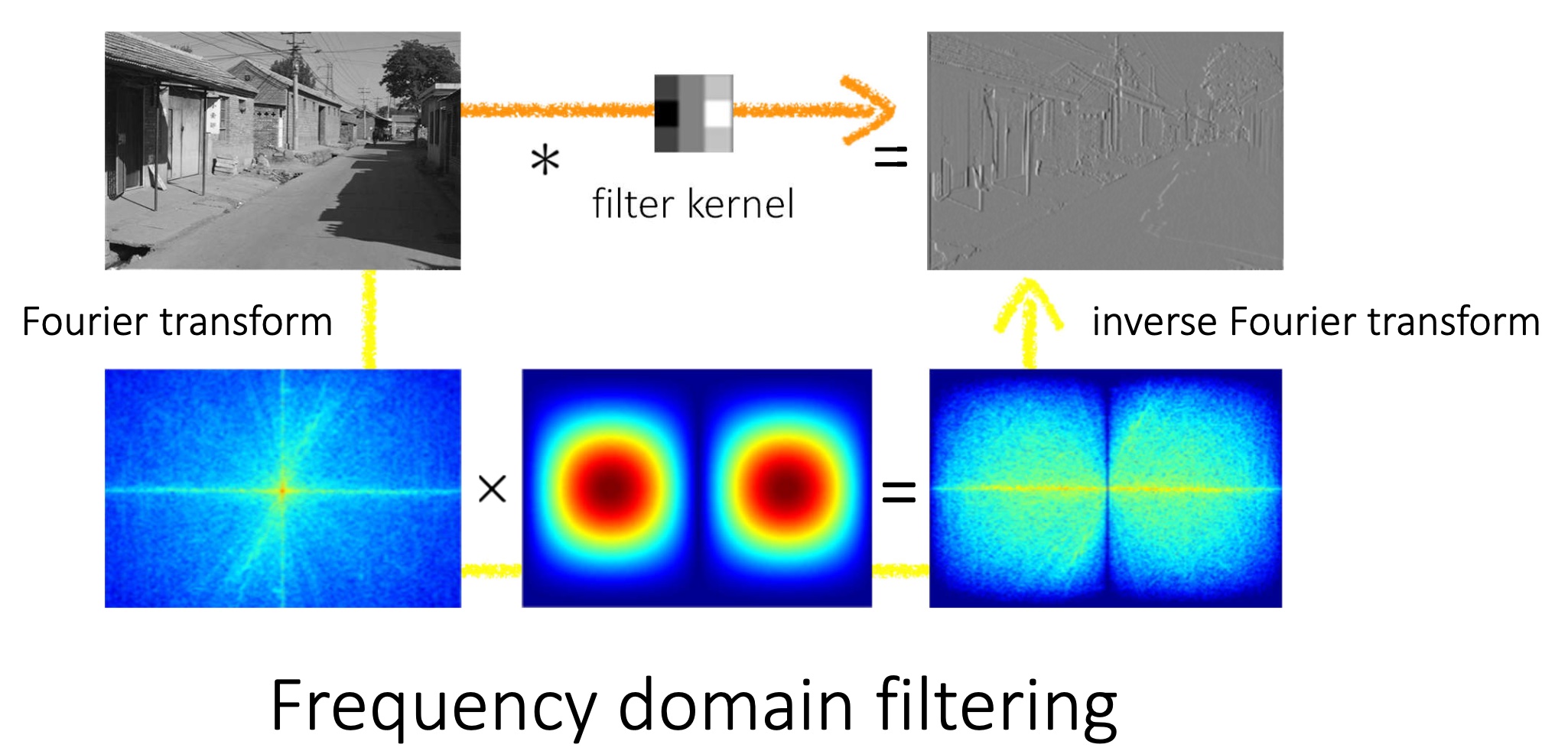
从这个角度也能理解为什么高斯核模糊化时效果很好,而正方形核模糊化会产生更大的边缘效应。
The Nyquist-Shannon sampling theorem
表达: 连续的信号若要被离散形式很好地插值出来,则要求 $f_s\geq 2f_{\max}$,其中 $f_s$ 为采样频率,$f_{\max}$ 为最高频率。
换种表达方式,则是说,下采样时,只要满足该式子,则不会发生走样。
而高斯滤波器是低通滤波器,它让大量减少高频率片段的占比,所以能防止走样的出现。
人眼被中频主导。