Review of Course Computer Vision Lecture 10:Camera
为期末考试复习做个准备。
Lecture 10: Camera
Homogeneous coordinates:齐次坐标,对于一个坐标系 O-XYZ 而言,每个向量 $v$ 都会被表示成 $\mathbf{v}=v_1\mathbf{x}+v_2\mathbf{y}+v_3\mathbf{z}$,每个点 $p$ 都可以被表示成 $p=p_1\mathbf{x}+p_2\mathbf{y}+p_3\mathbf{z}+o$。于是,此时为了用矩阵表达,统一地会设 $\mathbf{v}=(v_1,v_2,v_3,0),p=(p_1,p_2,p_3,1)$,这样就可以用 $(\mathbf{x},\mathbf{y},\mathbf{z},o)$ 与之相乘获得坐标变换了。具体实现时,点的齐次坐标的第四维表达了整体的缩放比例,所以会将四个维度同时除以第四维以获得比较标准的齐次坐标。
Homographies:单应性变换,射影变换,即从一个平面投射到另一个平面的变换,一般可以被表示成一个齐次坐标与 $3\times 3$ 的非奇异矩阵 $H$ 的乘积。
在真实场景取景中,相机的拍摄就更像是射影变换,所以需要我们对相机的一些信息更加了解。
小孔成像
小孔成像中,随着光圈越来越小,摄像也会越来越清晰,但不能无止境变小光圈,一是会越来越暗(光越来越少),二是会产生衍射 (Diffraction) 现象。
后来就发明了透镜 (lens)。
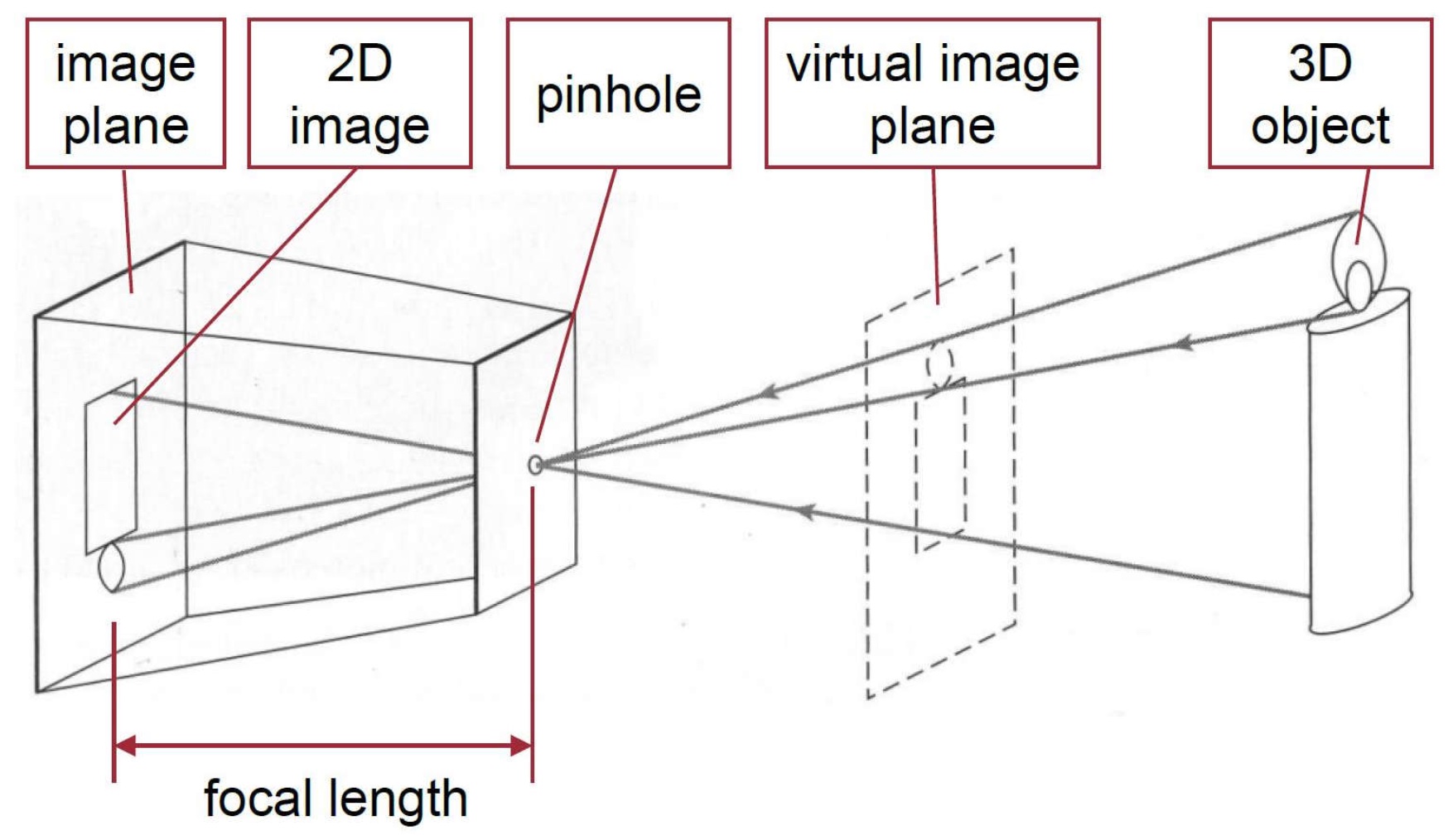
上图是小孔成像的示意图,相机就是把小孔换成了透镜。
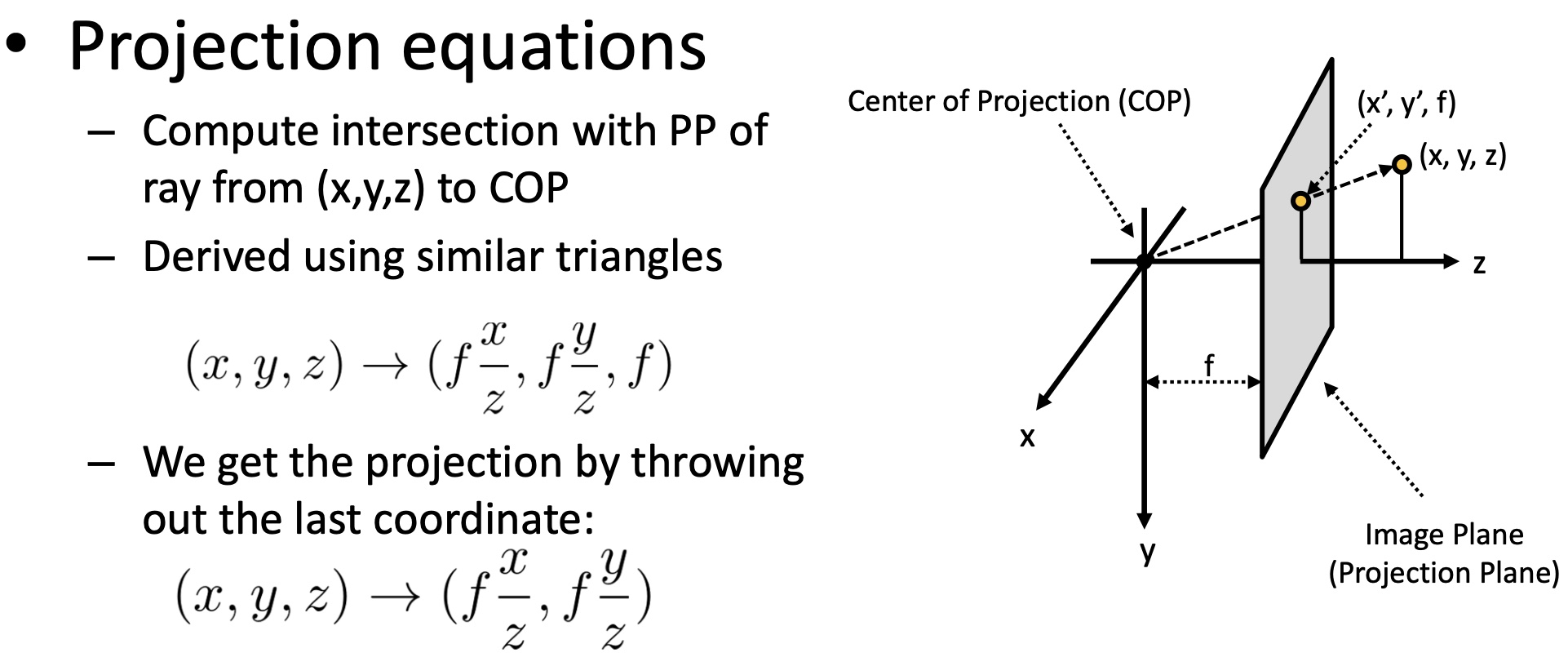
Image Plane 是虚像成的平面,COP 是光学中心/投射中心,也就是透镜的中心点。可以看到,$(x,y,z)$ 通过光学配件的投射之后会投射到 $(f\frac{x}{z}, f\frac{y}{z},f)$,由于 $f$ 是焦距,是定值,所以可以去掉,或者理解成在 Image Plane 处的坐标。
投影
Perspective Projection:透视投影,其对齐次坐标的操作为 $\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1/f & 0\end{pmatrix}\begin{pmatrix}x\\y\\z\\1\end{pmatrix}=\begin{pmatrix}x\\y\\z/f\end{pmatrix}\implies \begin{pmatrix}fx/z\\fy/z\end{pmatrix}$。
可以发现投射矩阵乘某个常数不会影响最终变化出的结果。
Orthographic projection:垂直投影,是一种特殊的 Perspective Projection,等价于让 $f\to \infty$?最后会得到矩阵的极限为 $\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 1\end{pmatrix}$。
垂直投影也有放缩形式 (Scaled orthographic),即投影矩阵为 $\begin{pmatrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 1/d\end{pmatrix}$,也被称为弱射影 (weak perspective)。
仿射投影 (Affine projection) 则是 $\begin{pmatrix}a & b & c & d\\e & f & g & h\\0 & 0 & 0 & 1\end{pmatrix}$,也被称为参数式投影 (paraperspective)。
3D 投影到了 2D 损失了两个信息:角度和距离。
Projection properties:
- Many-to-one: any points along same ray map to same point in image.
- 点到点。
- 线到线,或者退化成点。
- 面到面,或者退化成线。
相机参数
有三种参考系,分别是世界,相机和图像。

拍照等价于如上图的步骤,世界到相机需要知道在世界参考系下相机的位置和方向 (相机外参,extrinsics),相机到图像需要知道相机内参 (intrinsics)。
相机外参有两部分组成,一是向量 $\mathbf{T}$,表示光学中心到世界参考系原点的位移量 (Translation);二是矩阵 $\mathbf{R}$,表示 image plane 的旋转。
相机内参有三部分组成,一是焦距 (focal length) $f$;二是像主点 (principal point) $(c_x,c_y)$,即光学中心与 image plane 垂线与 image plane 的交点;三是 pixel aspect size $\alpha$,是像素的比例参数。
设 $\mathbf{X}=\begin{pmatrix}x\\y\\z\\1\end{pmatrix}$ 为世界参考系下的坐标,$\mathbf{x}=\begin{pmatrix}sx\\sy\\s\end{pmatrix}$ 为图像参考系下的坐标,则有变换公式为
$$
\mathbf{x}=\mathbf{\Pi}\mathbf{X}.
$$
其中,$\mathbf{\Pi}$ 表示如下。
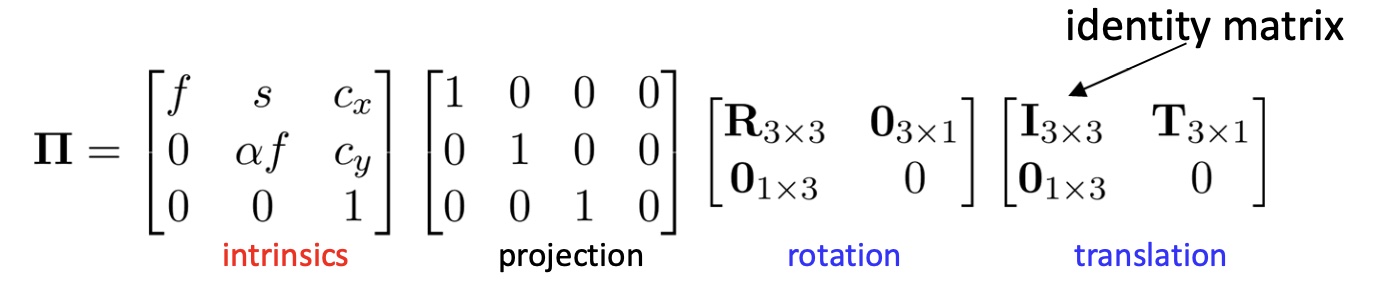
注意: 这些参数的定义并不标准唯一,不同课本有不同定义。
在 NERF 中,相机外参一般会选择逆变换,即从相机参考系变换到世界参考系,矩阵表示为
$$
\begin{pmatrix}\mathbf{R} & \mathbf{T}\\0 & 1\end{pmatrix}.
$$
其中,$\mathbf{R}$ 的第一列到第三列分别表示了相机坐标系的 X, Y, Z 轴在世界坐标系下对应的方向,$\mathbf{T}$ 表示的是相机原点 (光学中心) 在世界坐标系的对应位置。
相机内参中,$\alpha$ 是 aspect ratio,一般为 $1$,除非像素点不是正方形;$s$ 是 skew,一般为 $0$,除非像素点形状是菱形/平行四边形;$(c_x,c_y)$ 是 principal point,一般为 $(w/2,h/2)$,除非垂直点不是中心点。
焦距
短焦距 (wide angle) 拍摄的景更广,长焦距 (telephoto) 更窄。
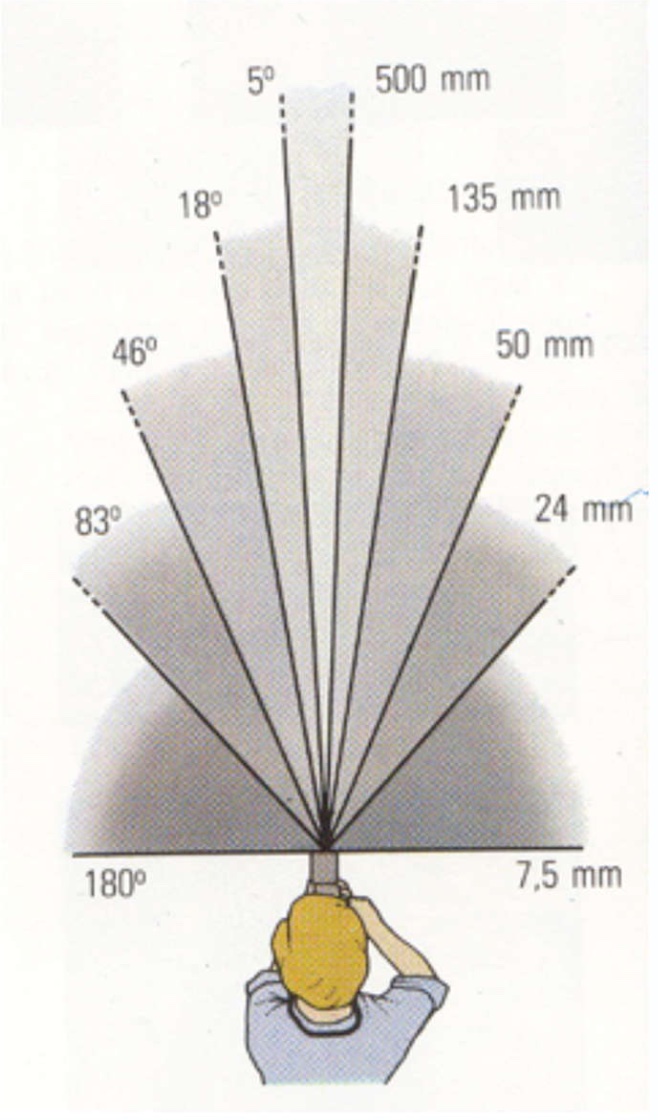

透视畸变 (Perspective distortion)
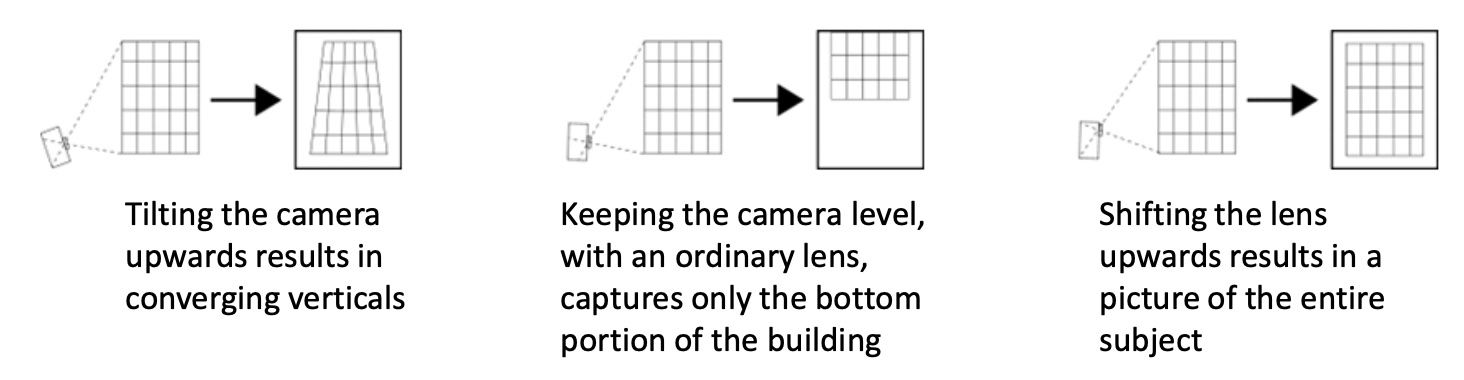
普通的畸变:因为拍摄角度导致的某种形状畸变,解决方法是使用特殊的摄像机 (view camera)。
Radial Distortion: 由不完美的镜头导致的,偏差对光线穿过镜头边缘十分敏感。
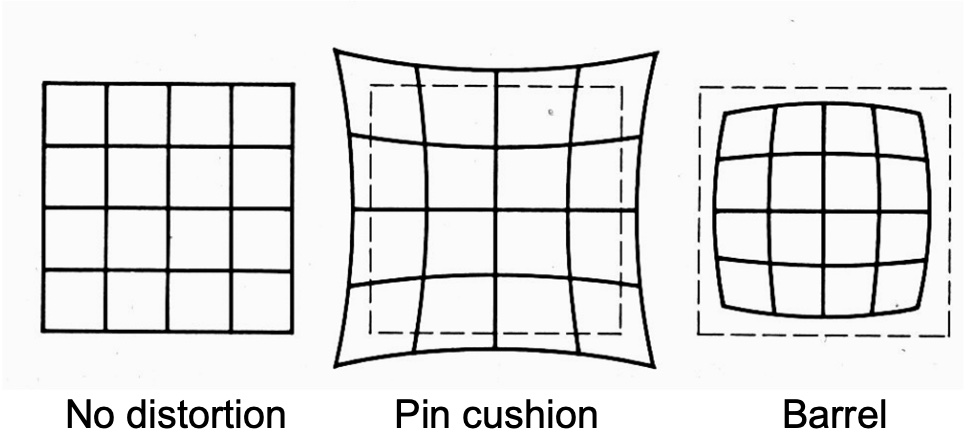
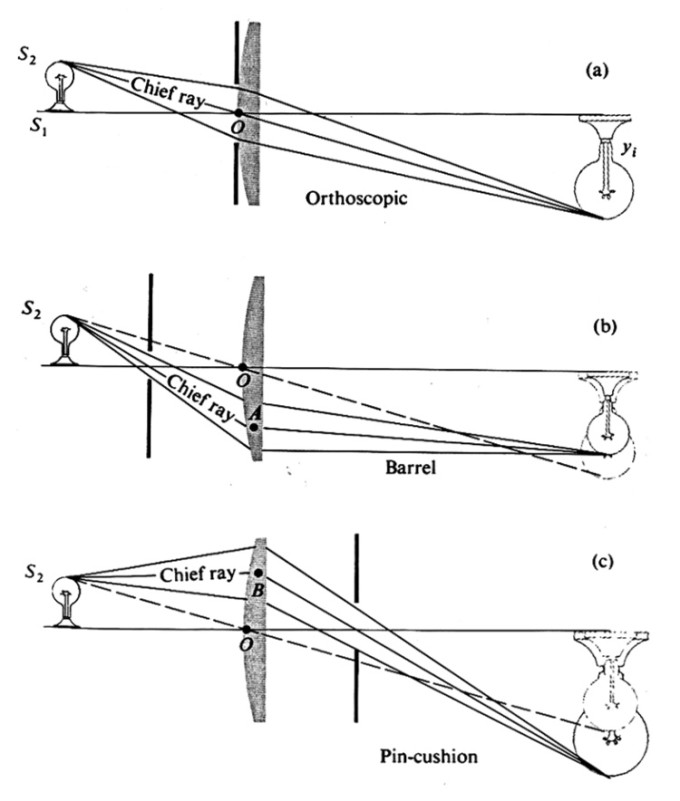
对于 Radial Distortion,他的畸变程度和某一点与中心的距离 $r$ 的偶次幂的和成正比,$r^2=(u-u_O)^2+(v-v_O)^2$。对于大多数的镜头,到二阶就足够了,即
$$
\begin{pmatrix}u_d\\v_d\end{pmatrix}=(1+k_1r^2)\begin{pmatrix}u-u_O\\v-v_O\end{pmatrix}+\begin{pmatrix}u_O\\v_O\end{pmatrix}.
$$
其中,$(u_d,v_d)^T$ 是未矫正的坐标。
更高阶的公式是:
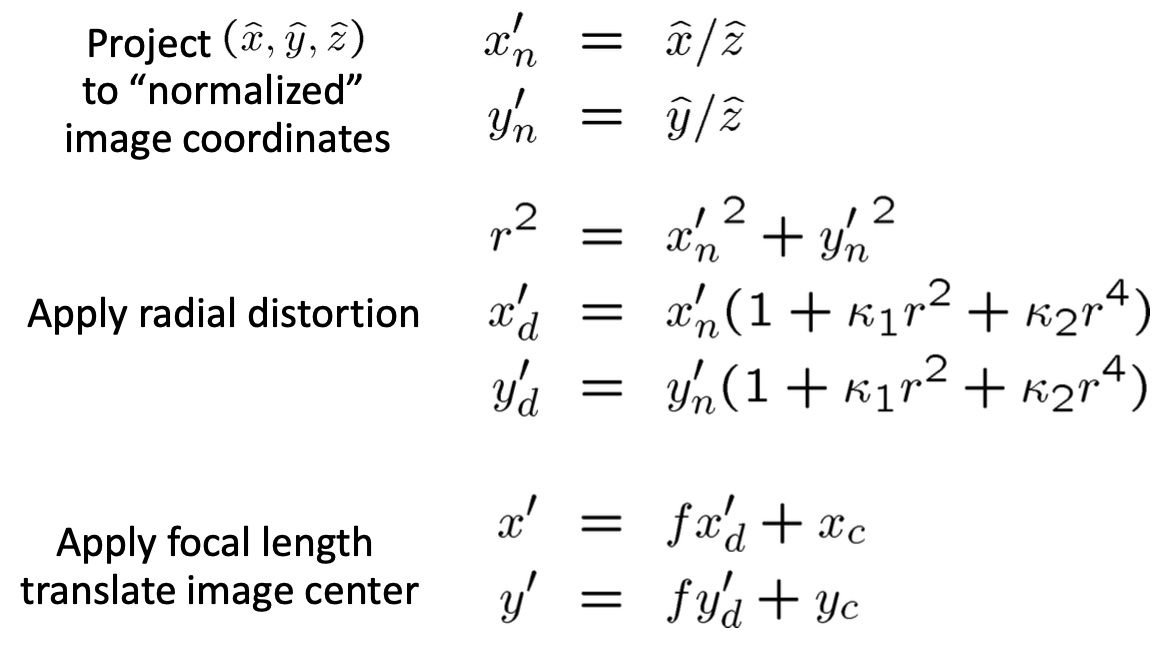
360 degree panorama
一个简单的拍摄全景思路为拿着镜头转一圈。

具体步骤如下:
- 拿着相机以固定的光学中心旋转拍出图像序列。
- 计算第一张和第二张图像的变换。
- 变换第二张去覆盖第一张。
- 融合两张获得一张 mosaic。
- 不断重复操作 2 3 4。
这种方式的几何理解是,投影图像从一个平面到另一个平面,投射性位移是与场景独立的。
那么如何去计算两张图像间的联系呢?等价于如何去计算像素点之间的映射呢?
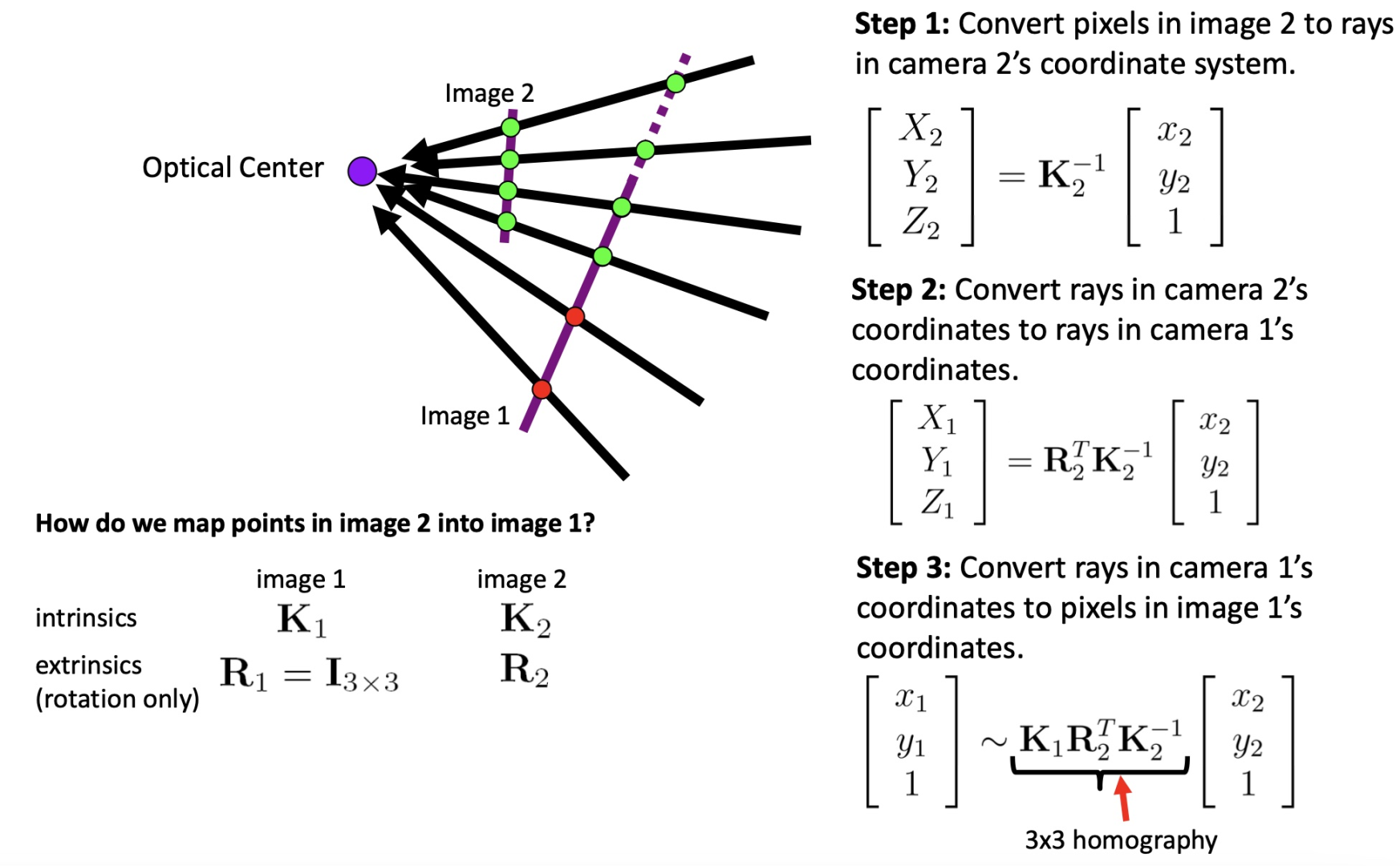
大致思路就是转换到相机参考系后,通过不同的旋转矩阵进行变换。
但实际上单应性变换并不能获得 $360$ 度的全景,需要利用球体投影 (Spherical projection) 才可以。
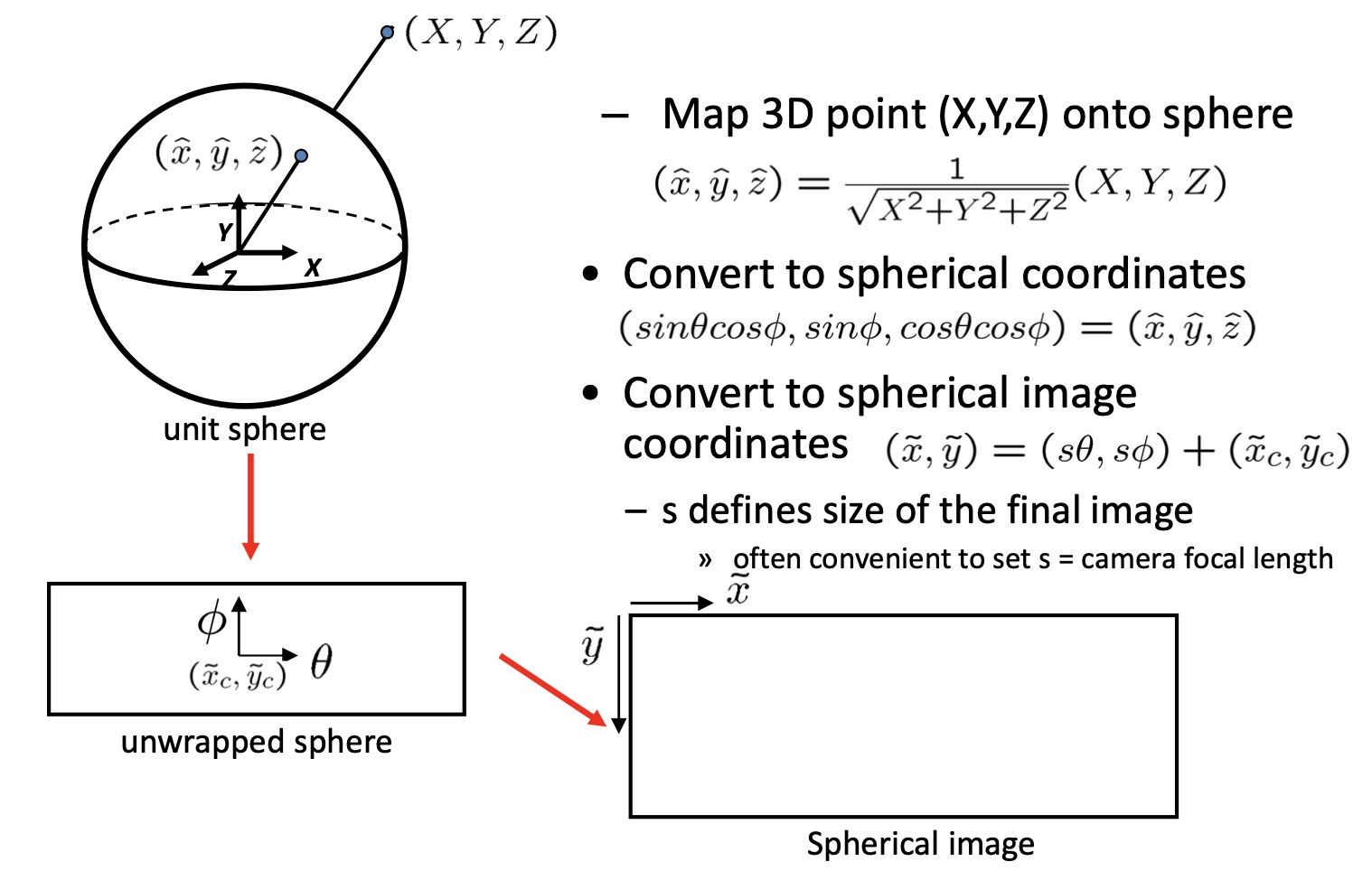
球坐标系下,相机的旋转等价于 $\theta$ 的平移。
类似之前的,只不过用球体投影做出了新的融合图像序列。
但融合存在一些 error accumulation (随着拍摄变多而不断增加),为了减少这些 error,有以下几种做法:
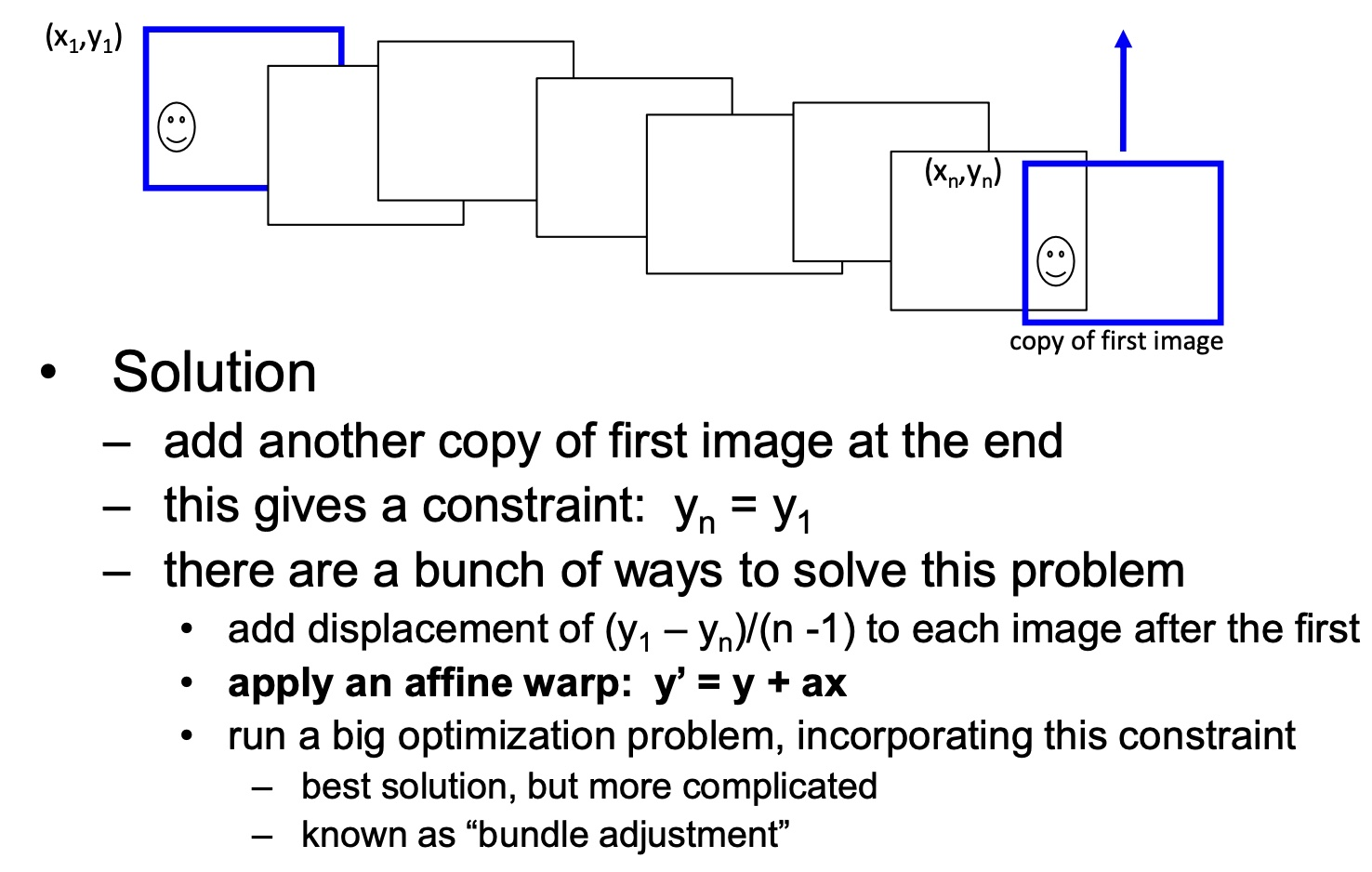
Blending
图像融合是为了去除两图像之间不太融洽的地方,有以下几个比较经典的思路:
- Create a Laplacian pyramid, blend each level.
- Alpha Blending: 思路是平均颜色。$\alpha$ 为零时为完全透明。
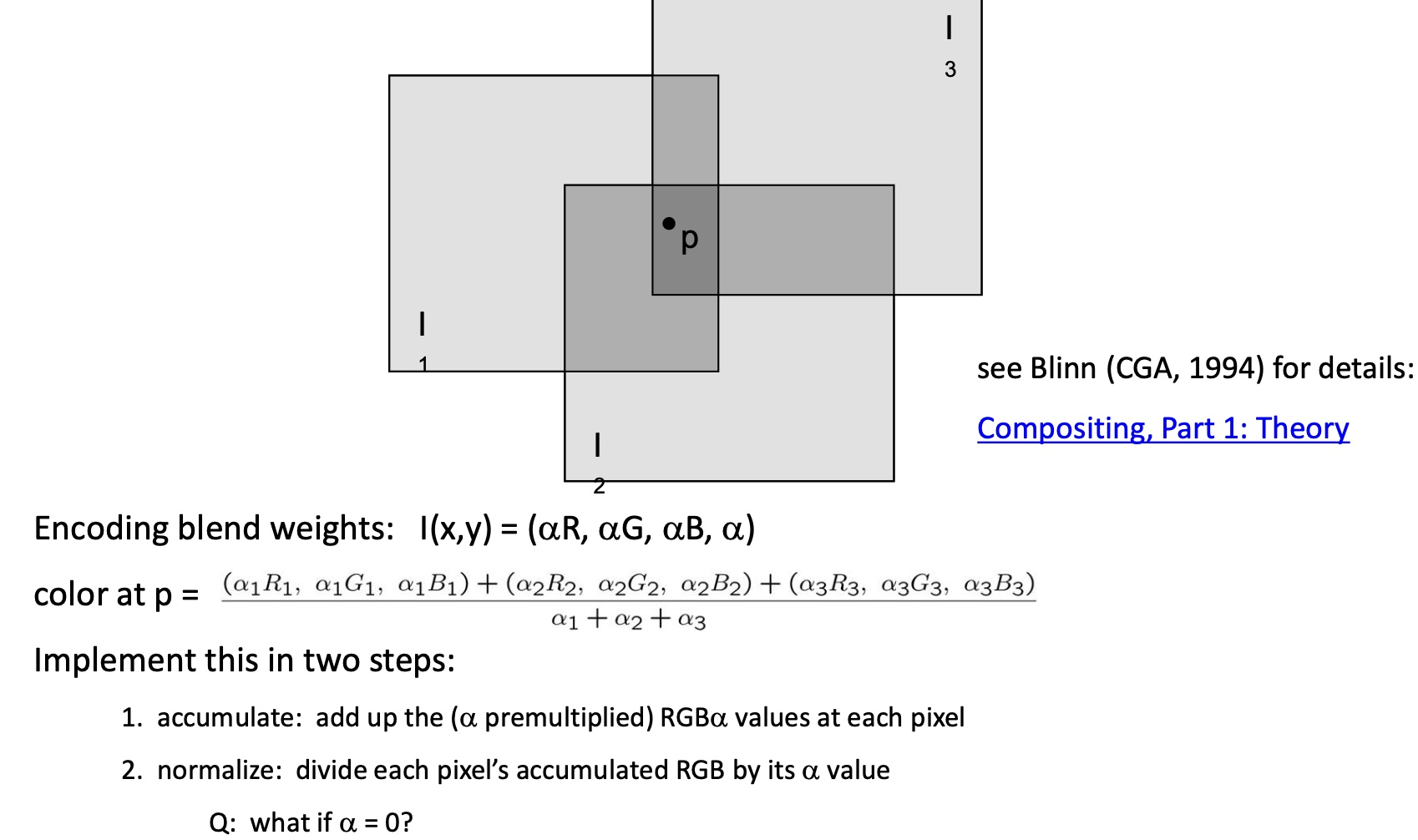
- Poisson Image Editing:将图像看作连续函数,融合图像就是最小化两个连续函数分界点处的差别,可以用求导等操作做成最优化问题。