Understanding the Unstable Convergence of Gradient Descent
这篇论文的地址,其主要思路和启发应该来自于 Lee et al., 2016.
Lee 的这篇论文证明了在一些合理的假设下,绝大多数情况下(概率为 $1$,非法情况的测度为 $0$),GD 从随机起点开始在经过足够次数的迭代后会收敛到一个非鞍点的驻点。采取的思路主要是依据 dynamical systems theory 和 Stable Manifold Theorem。而这篇论文进一步探讨不稳定收敛的情况。
Abstract
现有的大多数 (S)GD 分析依赖于一个条件:cost 函数是 $L-$smooth 的,此时要求步长小于 $\frac{2}{L}$。然而,在机器学习应用中,步长常常不满足这个条件,但 (S)GD 仍然能够收敛,尽管不稳定。该文从基本原理出发,调查了这种不稳定收敛现象的主要原因,并探讨了其主要特征及其相互关系。
梯度下降 (GD, Gradient descent)
GD 基于某种迭代的思路,即
$$
\mathbf{\theta}^{t+1}=\mathbf{\theta}^t-\eta \nabla f(\mathbf{\theta}^t).
$$
基于该迭代,去优化 cost 函数 $f$。
SGD 的区别就在于没有对所有样本求梯度,而是选取部分来求。
很多文献在分析 (S)GD 时会假设 $f$ 是 $L-$smooth (Lipschitz-smooth) 的,即
$$
\Vert \nabla f(\mathbf{\theta})-\nabla f(\mathbf{\theta’})\Vert\leq L\Vert \mathbf{\theta}-\mathbf{\theta’}\Vert, \text{for all $\mathbf{\theta}, \mathbf{\theta’}$}.
$$
可以简单理解为对导数做了个斜率限制,也在一定程度对二阶导数情况进行了限制。
在这个假设的基础上,能导出一个小引理。
下降引理 (Descent Lemma)
Description:若函数 $f$ 满足 $L-$smooth,则有
$$
f(\mathbf{\theta’})\leq f(\mathbf{\theta})+\nabla f(\mathbf{\theta})^{T}(\mathbf{\theta’}-\mathbf{\theta})+\frac{L}{2}\Vert \mathbf{\theta’}-\mathbf{\theta}\Vert^2.
$$
Proof Idea:$L-$smooth 给出了某种梯度之差的关系,而要求的是函数之差的关系,一个思路便是直接 Taylor 展开。
Proof:对 $f(\mathbf{\theta’})$ 进行 Taylor 展开,然后利用 $L-$smooth 进行放缩,即
$$
\begin{align*}
f(\mathbf{\theta’})=f(\mathbf{\theta})+\nabla f(\mathbf{\theta})^T(\mathbf{\theta’}-\mathbf{\theta})+\frac{1}{2}(\mathbf{\theta’}-\mathbf{\theta})^T\nabla^2 f(\mathbf{x})(\mathbf{\theta’}-\mathbf{\theta})\\
\leq f(\mathbf{\theta})+\nabla f(\mathbf{\theta})^T(\mathbf{\theta’}-\mathbf{\theta})+\frac{L}{2}\Vert \mathbf{\theta’}-\mathbf{\theta}\Vert^2.
\end{align*}
$$
Descent Lemma 的一个作用就是可以在 GD 时给出一个限制,即
$$
f(\mathbf{\theta}^{t+1})\leq f(\mathbf{\theta}^{t})-\eta (1-L\eta/2)\Vert \nabla f(\mathbf{\theta}^t)\Vert^2.
$$
这个的证明是容易的,代入 GD 的定义和 Descent Lemma 即可。
这个不等式给出了一个很好的限制,即如果为了每次迭代都能稳定让 cost 下降的话,则要求
$$
L<\frac{2}{\eta}.
$$
我们称步长满足该式时为稳定区域。
实际上不稳定收敛的情况十分常见。在二次函数中,似乎稳定区域的限制是必要的。这一观察统一在了大多数凸优化的情况,以及应用神经正切核 (NTK, Neural Tangent Kernel) 的神经网络中。但在一般的非凸 cost 的情况下,尚不清楚稳定区域条件是否必要或合理。
而在近期的应用中,Cohen et al. (2021) 观察到应用 GD 训练 NN 时经常不满足稳定区域条件,但训练仍然在收敛。这种现象被称为不稳定收敛。
Unstable GD Can’t Reach Stationary Points
有一个通过矩阵求导很容易得到的事实:
Fact 1
Description:对于一个二次 cost 函数 $f(\mathbf{\theta})=\frac{1}{2}\theta^TP\theta+\mathbf{q}^T\theta+r$ 而言,当 $P$ 的最大特征值大于阈值 $\frac{2}{\eta}$ 时,GD 会发散。当 $f$ 为凸时,该条件为充要条件。
Proof Idea:思路还是比较顺畅的,利用上述性质可以想到求导。
Proof:对 $f$ 求导,有
$$
\nabla f=\frac{1}{2}(P+P^T)\theta+\mathbf{q}.
$$
利用稳定区域的结论,以及 $L-$smooth 的定义,于是
$$
\Vert \frac{(P+P^T)}{2}(\theta-\theta’)\Vert\leq L\Vert\theta-\theta’\Vert\implies \Vert \frac{P+P^T}{2}\Vert=\lambda_{\max}\leq L<\frac{2}{\eta}.
$$
于是就导出了前半部分的结论。
后半部分限定了 $P+P^T$ 是正定的,正定限制了特征值均为正数。代入 GD 的迭代式子,即
$$
\theta^{t+1}=(I-\eta(\frac{P+P^T}{2}))\theta^t-\eta \mathbf{q}.
$$
此时充要条件的另一部分也就得证了。
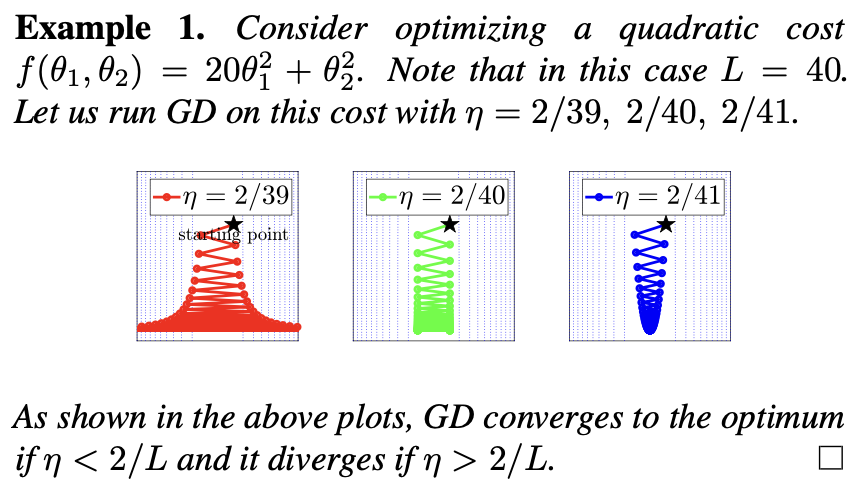
论文中给出了一个例子,可以明显看到是符合上述的数学证明的。
在这里先给出一个关于 sharpness 的定义:
Definition (Sharpness)
一个点 $\theta$ 处的 sharpness 被定义为
$$
\lambda_{\max}(\nabla^2 f(\theta^t)).
$$
这样来看,我们可以根据之前的信息有这样一个直觉猜测:
Intuition 1
当一个驻点的 sharpness 大于 $\frac{2}{\eta}$ 时,GD 没法收敛到这个点。
接下来,我们能证明这个 Intuition 在某些假设下是能做到绝大多数成立的。
Assumption 1
设 $F(\theta)=\theta-\eta\nabla f(\theta)$,我们做出以下假设:
对任意的零测度集合 $S$,$F^{-1}(S)$ 也一定是零测度的。
更进一步,我们可以假设对任意一个驻点 $\mathbf{p}$,满足 $\frac{1}{\eta}\not\in \lambda(\nabla^2f(\mathbf{p}))$,其中 $\lambda(\nabla^2f(\mathbf{p}))$ 表示的是 $\mathbf{p}$ 处的 $f$ 的 Hessian 矩阵的特征值集合。
这个假设的目的是为了接下来的定理证明,由此得到 Intuition 1 的合法性。
接下来先介绍一个比较重要的引理:稳定流形定理 (Stable Manifold Theorem)。
Lemma 1 (Stable Manifold Theorem)
Description:设 $\mathbf{p}$ 是一个确定的点,$h:U\rightarrow \mathbb{R}^n$ 是一个 $C^r(r\geq 1)$ 的局部微分同胚,其中 $U$ 是 $\mathbf{p}$ 的一个开邻域。设 $E^s\oplus E^c\oplus E^u$ 是 $\mathbb{R}^n$ 的不变分解,分别对应 $Dh(\mathbf{p})$ 的绝对值小于 $1$ 或等于 $1$ 或大于 $1$ 的特征值的广义特征空间 (直和分解定理)。
有引理如下:对于 $Dh(\mathbf{p})$ 不变子空间 $E^s\oplus E^c$,存在一个关联的局部 $h$ 不变且 $C^r$ 的嵌入盘 $W^{s\oplus c}{\text{loc}}$,其维度为 $\dim(E^s\oplus E^c)$。如果对于某个 $\mathbf{x}$,$h^n(\mathbf{x})\in B,\forall n\geq 0$,其中 $B$ 是 $\mathbf{p}$ 附近的开球,则 $\mathbf{x}\in W^{s\oplus c}{\text{loc}}$。
Understanding:这个引理揭示了一个比较重要的东西,就是若一个点的迭代变化是稳定或中性的,且它始终在某一个收敛点迭代,则它一定会在一个 $h$ 下不变的盘中。在 GD 中,将 $\mathbf{p}$ 理解成某个驻点,则可以进一步了解迭代收敛过程。
Theorem 1
Description:对于一个给定的 $\mathcal{X}$,它是参数 $\theta$ 的值域的子集,假设 $f$ 在 $\mathcal{X}$ 内是二阶可微的。假设对于 $\mathcal{X}$ 中的每个驻点 $\mathbf{p}$,满足要么 $\lambda_{\min}(\nabla^2 f(\mathbf{p}))<0$,要么 $\lambda_{\max}(\nabla^2 f(\mathbf{p}))>\frac{2}{\eta}$。那么在 Assumption 1 的前提下,一定存在一个零测度的子集 $\mathcal{N}$,满足对于所有初始点 $\theta_0\in \mathcal{X}\backslash \mathcal{N}$,GD 不能收敛到任何在 $\mathcal{X}$ 中的驻点。
Understanding:首先观察下这个 $\mathcal{X}$ 是什么,可以发现,$\lambda_{\min}$ 的条件是鞍点的意思,而 $\lambda_{\max}$ 的条件则就是我们所要的 sharpness。比对 Lee et al., 2016,可以发现这里的改进就在于对 sharpness 的分析。另一方面,它表达了除了一个零测度集以外,其余情况都在 Assumption 1 下满足了我们的 Intuition 1,也就是绝大部分初始点都会满足 Intuition 1。
Proof Idea:证明这个定理的思路借鉴了 Lee et al., 2016,仍然是考虑 Lemma1(Stable Manifold Theorem) 来导出我们想要的结果。主要是利用 $W^{s\oplus c}_{\text{loc}}$ 的可数并来构造 $\mathcal N$。
Proof:要运用 Lemma 1,我们需要先证明 GD 中的 $F(\theta)=\theta-\eta\nabla f(\theta)$ 在每一个满足 $\frac{1}{\eta}\in \lambda(\nabla^2 f(\mathbf{p}))$ 的驻点 $\mathbf{p}$ 处都是个局部微分同胚。这利用反函数定理,即考虑其 Jacobian 矩阵可逆情况。首先由于 $f$ 是 $C^2$,所以 $F$ 是 $C^1$,保证了可导;另一方面,$DF(\mathbf{p})=I-\eta\nabla^2 f(\mathbf{p})$,又因为 $\frac{1}{\eta}\not\in \lambda(\nabla^2 f(\mathbf{p}))$,所以 $DF(\mathbf{p})$ 是可逆。这就证明了 $F$ 在 $\mathbf{p}$ 处是个局部微分同胚。
这样就可以使用 Lemma 1 了。对于每个满足 $\frac{1}{\eta}\not\in \lambda(\nabla^2 f(\mathbf{p}))$ 驻点 $\mathbf{p}$ 考虑 Lemma 1。即设 $B_{\mathbf{p_i}}$ 是驻点 $\mathbf{p_i}$ 的开球,设一个 $\mathcal{S}=\lbrace \mathbf{p}i\rbrace$ 的开覆盖
$$
\mathcal{C}=\bigcup{p_i\in \mathcal{S}\wedge \frac{1}{\eta}\not\in \lambda(\nabla^2 f(\mathbf{p}))} B_{\mathbf{p}i},
$$
利用 Assumption 1,可以知道 $\mathcal{C}$ 是 $\mathcal{S}$ 的一个开覆盖。利用 Lindelöf 定理 (第二可数空间的任意开覆盖都存在一个可数的子覆盖),则 $\mathcal{C}$ 一定存在一个可数子覆盖,即 $\mathcal{C}=\cup{i=1}^{\infty} B_{\mathbf{p}i}$。如果初始点为 $\mathbf{\theta_0}$ 的 GD 收敛于一个驻点 $\mathbf{p}$,则一定存在一个 $t_0,i$ 满足 $F^t(\theta_0)\in B{\mathbf{p}i},\forall t\geq t_0$。根据 Lemma 1,我们有 $F^t(\theta_0)\in W^{s\oplus c}{\text{loc}}(\mathbf{p}i),\forall t\geq t_0$。于是我们就能构造出 $\mathcal{N}$ 了,即
$$
\mathcal{N}=\bigcup{i=1}^{\infty}\bigcup_{t=0}^{\infty} F^{-t}(W^{s\oplus c}_{\text{loc}}(\mathbf{p}_i)),
$$
其中 $\mathcal{N}$ 的一个子集中的所有点作为初始点时会收敛到驻点 $\mathbf{p}$。
现在我们要证明 $\mathcal{N}$ 是零测度的。
在这个定理的假设中,有假定 $\lambda_{\min}(\nabla^2 f(\mathbf{p}))<0$ 或 $\lambda_{\max}(\nabla^2 f(\mathbf{p}))>\frac{2}{\eta}$,于是就保证了 $I-\eta\nabla^2 f(\mathbf{p})$ 的特征值的绝对值大于 $1$。于是对于每个驻点 $\mathbf{p}$,$\dim(E^u)\geq 1$,于是 $\dim(E^s\oplus E^c)\leq n-1$,也即 $W^{s\oplus c}{\text{loc}}$ 是零测度的,从 Assumption 1 中就又能知道 $F^{-1}(W^{s\oplus c}{\text{loc}})$ 也是零测度,也就是说 $\mathcal{N}$ 是可数个零测度集的并,于是 $\mathcal{N}$ 也是零测度的。也就证明了 Theorem 1。
Remark 1
定理不要求驻点一定是孤立的,同时 $\frac{1}{\eta}\not\in \lambda(\nabla^2 f(\mathbf{p}))$ 的条件可以放宽,它实际上仅仅保证了 $\mathcal{C}$ 是 $\mathcal{S}$ 的开覆盖,如果有其他方面可以走到这一步也是可行的。
接下来我们将探讨不稳定区域内要如何收敛的。
How Can Unstable GD “Converge”?
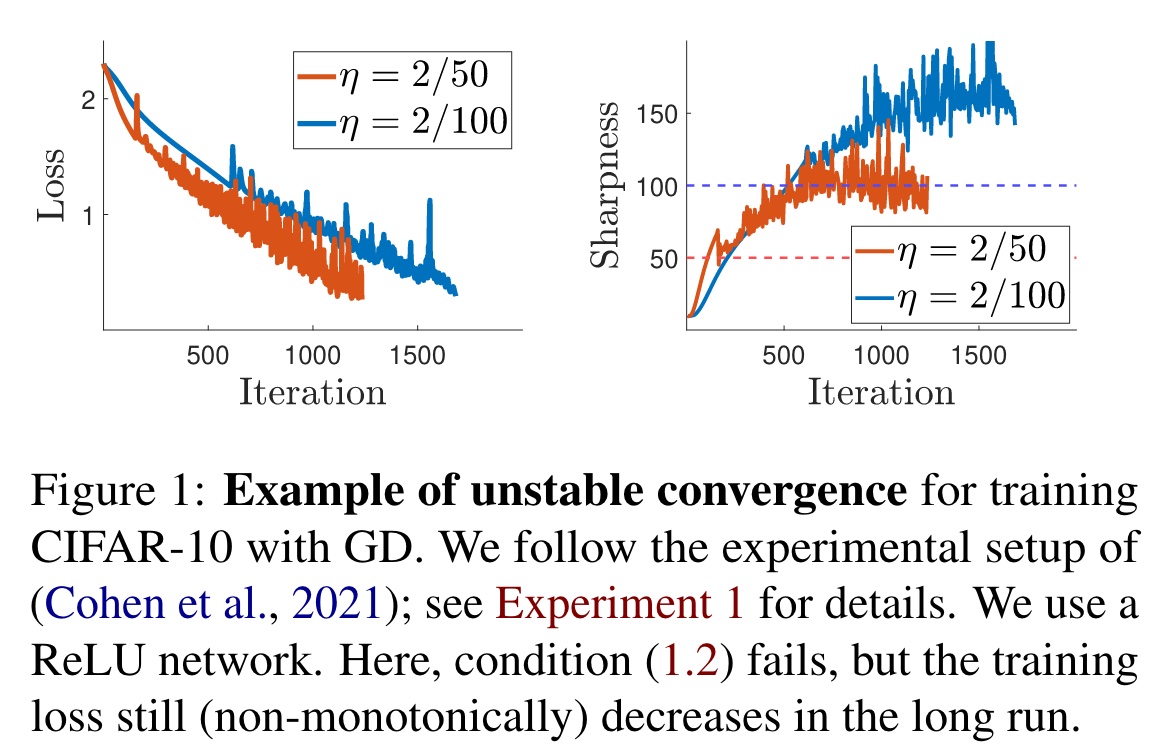
从这张图上来看,不稳定区域内 GD 也是可以做到收敛的。
Proposition 1
Description:设神经网络的损失函数 $\mathcal{L}(\theta)=\frac{1}{n}\sum_{i=1}^n f(\mathbf{x}_i,\theta)+\gamma\Vert \theta\Vert_2^2$,其中 $\mathbf{x}_i$ 为输入,$\theta$ 为神经网络参数。如果我们分割 $\theta=[\xi;\zeta]$,其中 $\zeta$ 是正齐次的,也就是说 $f(\mathbf{x}_i,[\xi,\zeta])=f(\mathbf{x}_i,[\xi,c\zeta]),\forall c>0$。于是 $\mathcal{L}(\theta)$ 不会有驻点除非 $\zeta=0$。
Understanding:在如 Transformer 或 ResNet 这类 NN 中,正齐次参数是常见的,而它存在时的收敛情况值得被研究。
Proof Idea:正齐次参数有个很好的内积性质,基于该性质可以证明。
Proof:正齐次参数一个很好的性质就是
$$
\langle \nabla_{\zeta}f(\mathbf{x}_i,[\zeta,\xi],\xi)=0.
$$
这个性质证明不难,考虑 $f(\mathbf{x}_i,[\xi,c\zeta])$ 在 $[\xi,\zeta]$ 处展开,因为正齐次性,所以意味着后面的每一项都得是 $0$,也就得证了。
如果 $\nabla_{\zeta}\gamma\Vert\theta\Vert_2^2\neq 0$,又 $\langle \nabla_{\zeta}\gamma\Vert\theta\Vert_2^2,\theta\rangle\neq 0$,这是因为 $\xi\neq 0$,直接代入可以证明的,那么 $\nabla_{\zeta}(f(\mathbf{x}_i,[\xi,\zeta])+\gamma\Vert\theta\Vert_2^2)\neq 0$,于是就得证了。
在 ResNet 或 Transformer 中,总有一些类似 $a_{L+1}=a_L/\Vert a_L\Vert$ 的层,这是正齐次化的,我们知道驻点事 $a_L=0$,但这时分式无定义,所以一般使用 $a_{L+1}=a_L/(\epsilon+\Vert a_L\Vert)$,这样的驻点在 $\Vert a_L\Vert=\epsilon$。但这时的 sharpness 的级别在 $\sim 1/\epsilon$,这样的级别太大了。
这也就导致了容易陷入不稳定区域,总结来说,就是过少的非平凡驻点导致容易陷入不稳定区域。
但很神奇的是,在不稳定区域时,有时也会“收敛”,接下来来从 Fact 1 探讨这个现象。

可以注意到 $\tanh$ 存在一个作用: forward-invariant,即如果 $S$ 基于 $F$ 变化,则 $F(S)\subseteq S$。$\tanh(x)\sim x,x\to 0$,于是在最小值处 $\tanh(\text{quadratic})$ 会有 forward-invariant 性质。

可以注意到在 NN 中,$\tanh$ 的加入使得网络收敛在了最小值处。虽然我们知道那个区域仍然是不稳定区域,但基于 $\tanh$ 的 forward-invariant 性质,它仍会在最小值处收敛。

从上表可以看出,只要神经网络的某一部分比如激活函数能在最小值处有 forward-invariant 性质,就可以使得 GD 不单调收敛进不稳定区域。
接下来我们探讨不稳定区域里收敛的特征。
Charateristics of the Unstable Convergence
我们先探讨 loss 的情况。
在前面,我们知道一个引理叫 descent lemma,即如果 GD 在稳定区域时,$f(\theta^{t+1})-f(\theta^t)\leq -c\eta \Vert \nabla f(\theta^t)\Vert^2$,$c$ 为某一大于 $0$ 常数。移项得到
$$
\frac{f(\theta^{t+1})-f(\theta^t)}{\eta\Vert \nabla f(\theta^t)\Vert^2}\leq -\text{const}.
$$
于是我们用 LHS 作为一个探讨对象。
Definition (Relative progress ratio)
定义 $\text{RP}(\theta)=\frac{f(\theta-\eta\nabla f(\theta))-f(\theta)}{\eta\Vert \nabla f(\theta)\Vert^2}$。
我们对 $\text{RP}$ 的分子使用 Taylor 展开,可以发现等于 $-1+\frac{o}{\eta\Vert \nabla f(\theta)\Vert^2}$,这一定程度上也描述了收敛时会遇到的一些情况。

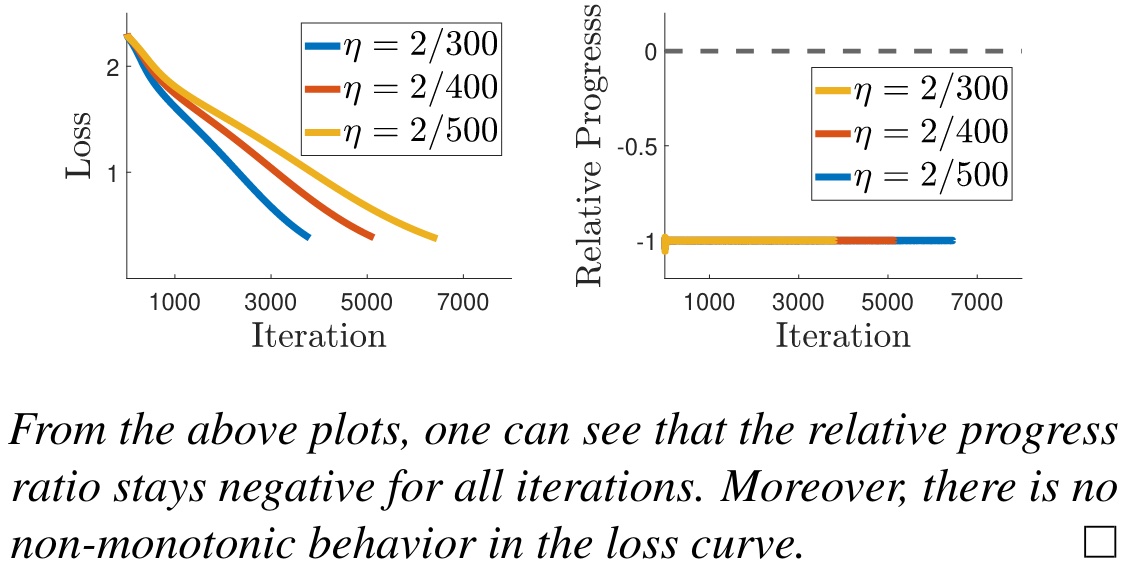
从结果来看,稳定区域的 $\text{RP}$ 结果与预测很符合,同时稳定区域内的收敛情况是单调的。
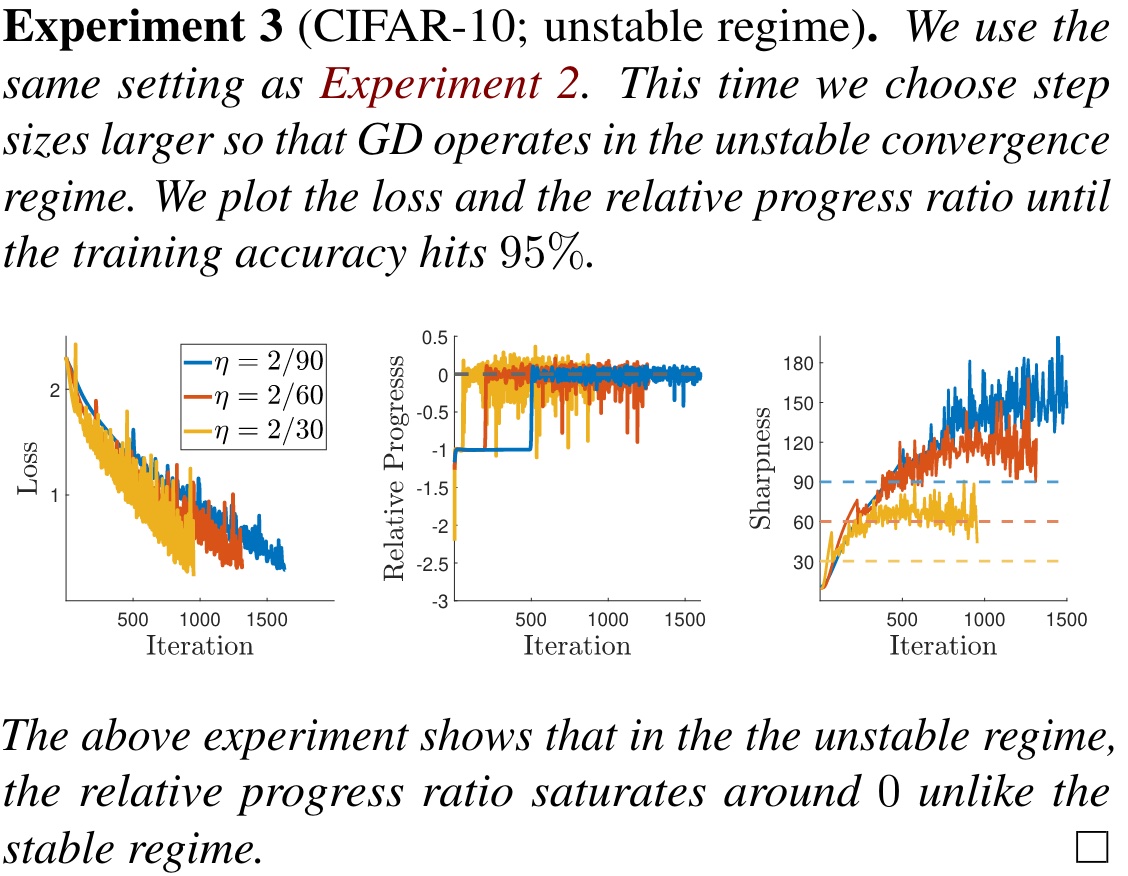
不稳定区域的情况就截然不同。$\text{RP}$ 会到达 $0$,而且收敛过程也不是单调的了。
从结果来看,步长 $\eta$ 越大时不稳定区域收敛效果更好,但过大则会发散,文中提到使用 $\eta=2/10$ 会发散。
注意到 $\nabla f(\theta-\mathbf{v})\approx -\nabla f(\theta)$,如果参数改变量 $\mathbf{v}$ 足够小则会出现这样的振荡现象。类似地,我们能给出一个定义
Definition (Directional smoothness)
定义
$$
L(\theta;\mathbf{v})=\frac{1}{\Vert \mathbf{v}\Vert^2}\langle \mathbf{v},\nabla f(\theta)-\nabla f(\theta-\mathbf{v})\rangle.
$$
代入 GD,即 $\mathbf{v}=\eta\nabla f(\theta)$,有
$$
L(\theta;\eta\nabla f(\theta))=\frac{\langle\nabla f(\theta),\nabla f(\theta)-\nabla f(\theta-\eta\nabla f(\theta))\rangle}{\eta\Vert \nabla f(\theta)\Vert^2}.
$$
当 GD 开始振荡时,$\eta\nabla f(\theta)$ 极小无比,根据前面描述,则 $L(\theta;\eta\nabla f(\theta))\approx \frac{2}{\eta}$。
考虑一个二次型 loss 函数 $f(\theta)=\theta^TP\theta$,其中 $P\succeq 0$。这样的情况下,$\theta^{t+1}=(I-\eta P)\theta^t$。考虑 sharpness,设 $P$ 的最大特征值和特征向量分别为 $\mathbf{q},\lambda$,于是有
$$
\langle \mathbf{q},\theta^t\rangle=\mathbf{q}^T(I-\eta P)\theta^{t-1}=(1-\eta \lambda)\langle\mathbf{q},\theta^{t-1}\rangle=(1-\eta\lambda)^t\langle\mathbf{q},\theta^0\rangle.
$$
这表明了如果 $\lambda<\frac{2}{\eta}$,$\langle \mathbf{q},\theta^t\rangle\to 0$。如果 $\lambda=\frac{2}{\eta}$,则 $\mathbf{q}^T\theta^t=(-1)^t\langle\mathbf{q},\theta^0\rangle$,也就是 $\theta^t=(-1)^t\langle \mathbf{q},\theta^0\rangle \mathbf{q},\forall t\geq N$,此时 $L(\theta;\eta\nabla f(\theta))=\frac{2}{\eta}$,发生振荡。
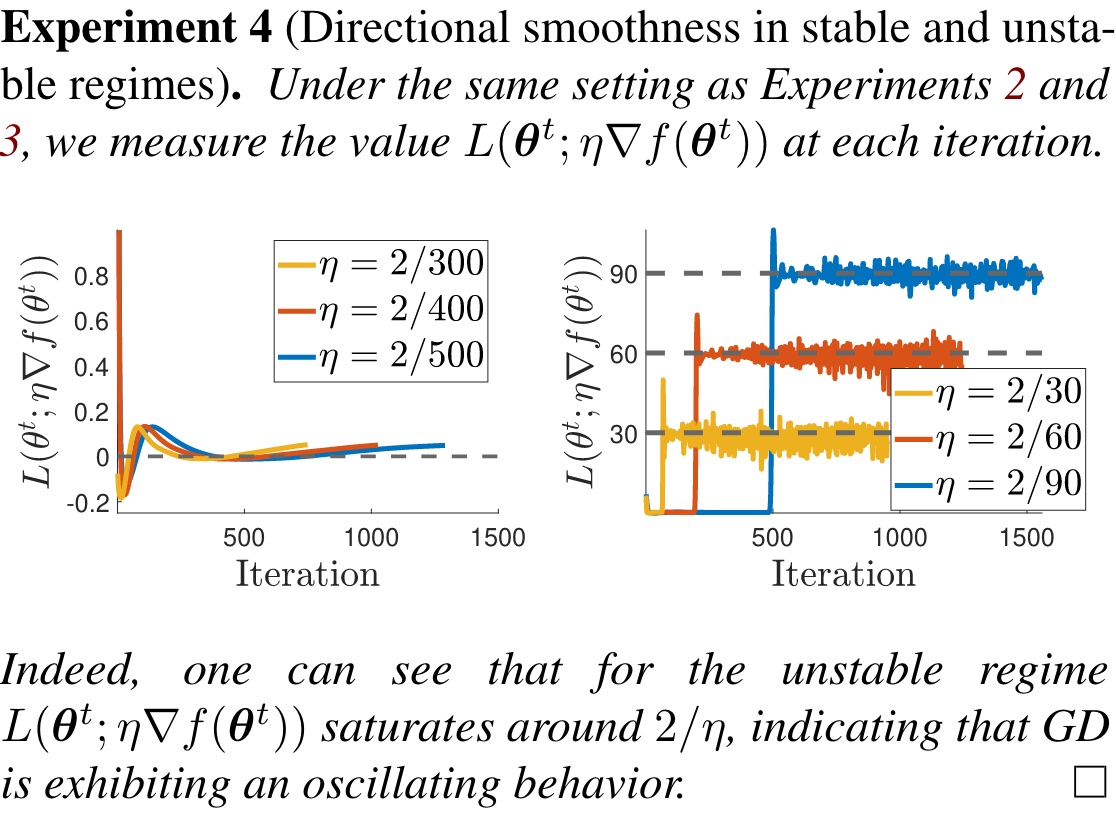
其实此刻根据上述分析,尤其是对 $\text{RP}$ 的 Taylor 展开,可以猜出一个近似公式
$$
\text{RP}(\theta)\approx -1+\frac{\eta}{2}L(\theta;\eta\nabla f(\theta)).
$$
确切公式只需要对 $f(\theta-\eta\tau \nabla f(\theta))$ 的 $\tau$ 求导即可得到
$$
\text{RP}(\theta)=-1+\eta\int_0^1 \tau\cdot L(\theta;\eta\tau\nabla f(\theta))\mathrm{d}\tau.
$$
也就很符合我们之前猜测的公式了。
非常有趣的点是,就算 Lipschitzness 性不是好的假设,但 Hessian 矩阵的 Lipschitzness 性仍然能有效。

接下来讨论 sharpness 在振荡时的变化。
根据参考文献 (Cohen et al., 2021),可以得知有两个结果被观察到
A. 大部分迭代时 $\lambda_{\max}(\nabla^2 f(\theta^t))>\frac{2}{\eta}$.
B. 在很多时候 $\lambda_{\max}(\nabla^2 f(\theta^t))$ 只是略微大于 $\frac{2}{\eta}$.
这两个性质一一来证明下,先证明 A。
设 $L_t=\sup_{\theta\in \overline{\theta^t\theta^{t+1}}}\lbrace \lambda_{\max}(\nabla^2f(\theta))\rbrace$,那么有 $\frac{2}{\eta}(\text{RP}(\theta)+1)\approx L(\theta;\eta\nabla f(\theta))\leq L_t$。
证明考虑使用 $L(\theta;\eta\tau \nabla f(\theta))$ 的定义和 $L_t$ 的关系即可。
这就可以说明了 A.
对于 B 而言,根据参考文献 (Arora et al., 2022),类似之前对二次型 loss 函数的操作,我们能知道 $t$ 足够大的时候 $\nabla f(\theta^t)$ 几乎平行于 $\nabla^2 f(\theta^t)$ 的最大特征向量。在这个基础上,$\lambda_{\max}(\nabla^2 f(\theta^t))$ 可以近似于 $\frac{2}{\eta}$。
Relative Progress for SGD
SGD 定义:$\theta^{t+1}=\theta^t-\eta g(\theta^t)$,满足 $E[g(\theta^t)]=\nabla f(\theta^t)$。
想要研究 SGD 的行为,一个合适的想法是对 $\text{RP}$ 进行研究。
定义 $E[\text{RP}(\theta)]=\frac{E[f(\theta-\eta g(\theta))]-f(\theta)}{\eta \Vert \nabla f(\theta)\Vert^2}$。
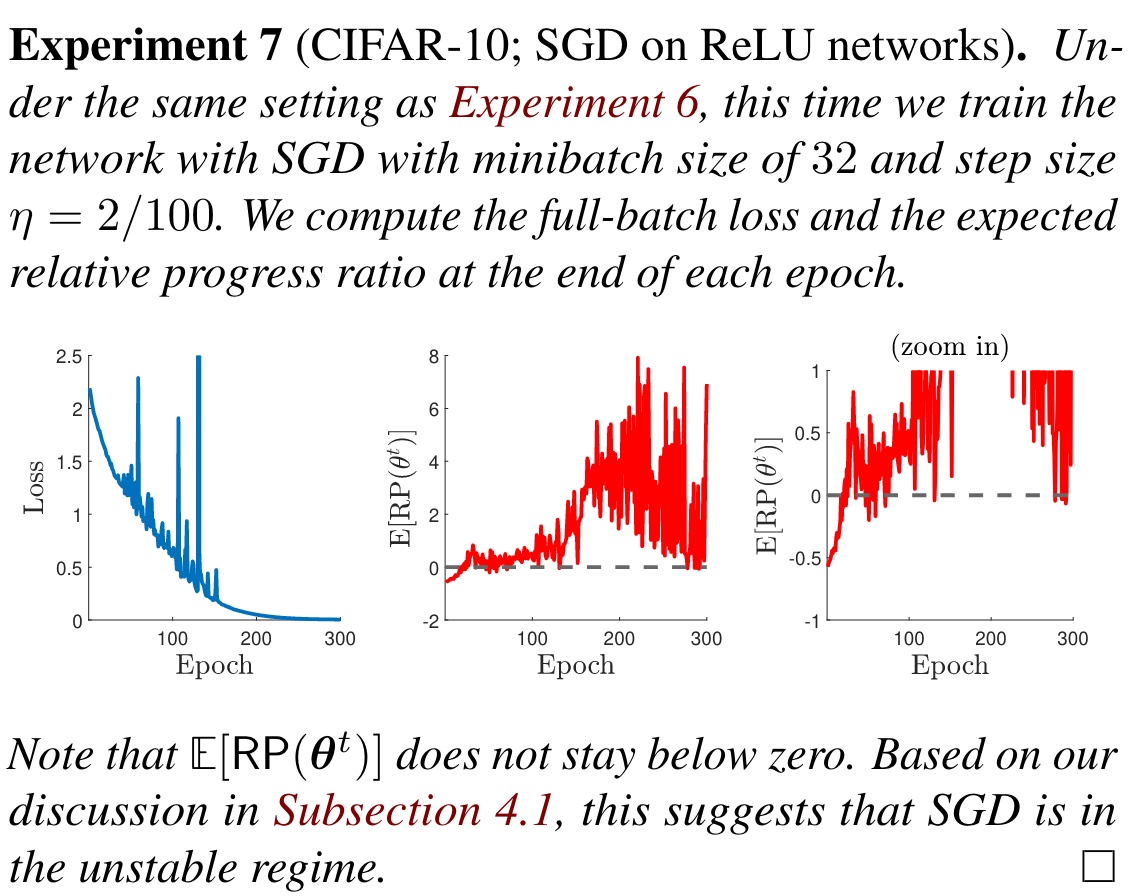
一个很神秘的事情是中途 loss 甚至会飙到很高,期望意义下居然不是稳定下降的。
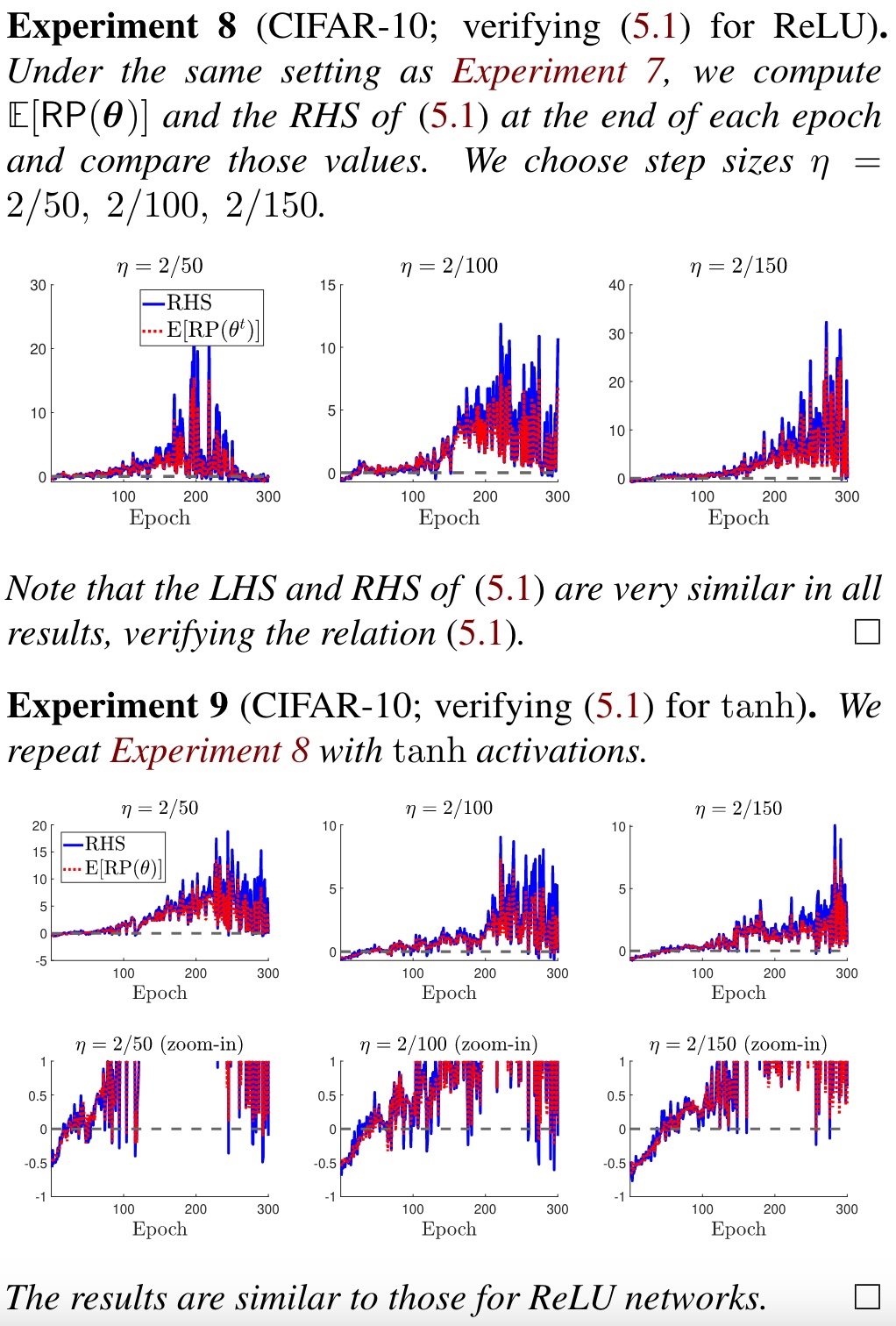
类似地,我们能得出 $\text{RP}$ 和 $L$ 的关系:
$$
E[\text{RP}(\theta)]=-1+\eta\int_0^1 \tau E_g[\frac{\Vert g(\theta)\Vert^2L(\theta;\eta\tau g(\theta))}{\Vert \nabla f(\theta)\Vert^2}]\mathrm{d}\tau\approx -1+\frac{\eta}{2}E_g[\frac{\Vert g(\theta)\Vert^2L(\theta;\eta g(\theta))}{\Vert \nabla f(\theta)\Vert^2}].
$$
Discussion and Future Directions
- 更好的 optimizer?
- 不稳定区域的收敛可以有更快的训练方式?比如步长加到正好的地步。
- 更改更好的假设?比如 Hessian 矩阵的 Lipschitzness 性质。
- 不稳定收敛使用一些自适应办法?